Galilean Invariance
Solutions to the fluid equations should be Galilean invariant, that is the same in every inertial frame. Recently, it has been reported that solutions generated by grid codes (like Athena) are not Galilean invariant. In fact, however, it is the test problems themselves that are flawed. They involve unresolved interfaces, so that solutions are dominated by truncation error, and it is this truncation error which violates Galilean invariance. We show below resolved solutions generated by Athena are invariant.
KH Instability Test
Initial Conditions
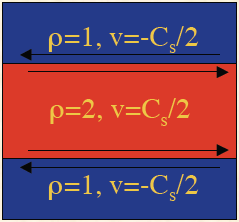
One of the problems used to test for Galilean invariance is the growth of the Kelvin-Helmholtz instability between two fluids of different densities. The interface between the fluids is an unresolved discontinuity (a slip-surface). The total velocity difference is equal to the sound speed $C_s$. The test is based on the KH instability test in the Athena test suite; the figure below sketches the initial conditions.
Results with Unresolved Interfaces
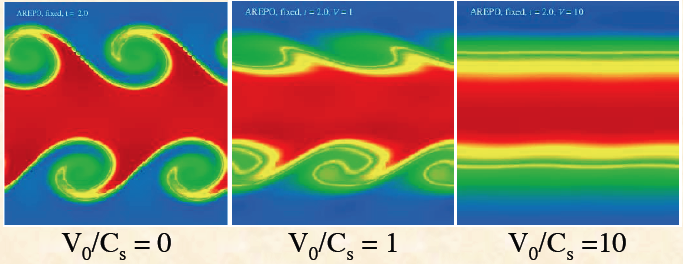
The images below show results typical of a grid code when the solution is computed in the rest frame (left), in a frame moving at the sound speed to the right (center), and a frame moving at ten times the sound speed to the right (right). Note the instability seems to disappear in the moving frames. This is because numerical diffusion at the interface damps the unstable modes.
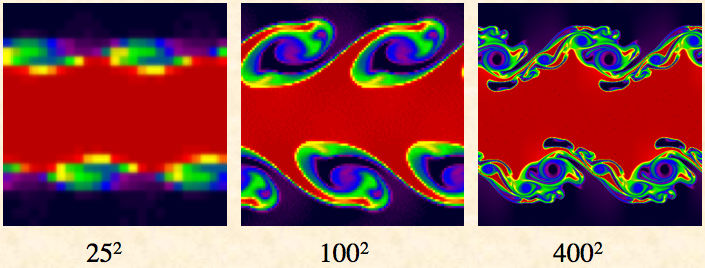
Of course, numerical diffusion is not only a problem in the moving frames. It also dominates the solution in the rest frame. The images below show the same test run at different resolutions in the rest frame. Note the solution is vastly different at each resolution, and the instability seems to disappear at the lowest resolution (where the truncation error is largest).
So which solution is correct? That is, which solution should the code reproduce in any inertial frame?. Of course, this question cannot be answered unless the test is based on a resolved solution.
Results with a Resolved Interface
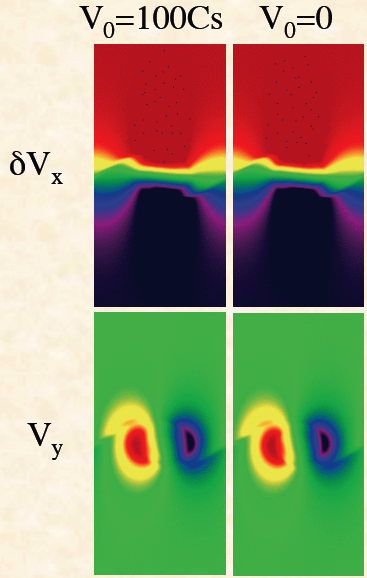
The images on the left below show the streamwise (x-direction), and spanwise (y-direction) velocity fluctuations from a test using uniform density, and in which the interface is spread out using a hyperbolic tangent function, with a characteristic scale a equal to twice the grid cell size. This replaces the discontinuity at the interface by a very sharp but smooth profile, and introduces a minimum lengthscale a in the problem that can be resolved. The images on the right are from a calculation in the rest frame, and on the left from a calculation moving at $100C_s$. This is even more extreme than the test above! Despite this, the images look identical.
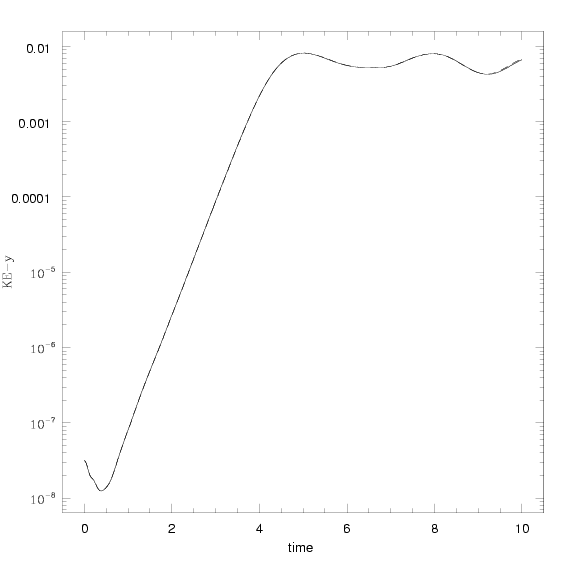
An even more quantitative test is to measure the kinetic energy associated with motion in the spanwise (y-) direction. There are two lines shown in the figure at left below, one taken from each calculation. It only appears there is one line, because the results are very nearly identical. In both cases, exponential growth in the linear regime is captured correctly.
Lessons Learned
Resolved solutions are Galilean invariant in Athena (although there will still be differences at the level of the truncation error).
The lack of invariance for unresolved solutions is because the truncation error is not Galilean invariant, and this truncation error dominates the solution.
The problem does not lie with the Riemann solver. After all, the fluxes of conserved quantities are different in different frames (although they are related by simple Galilean transformations).
Any algorithm that reduces diffusion at unresolved interfaces will improve the results of the slip-surface test shown above. This includes the contact steepener of Colella & Woodward (1984), or interface tracking methods, or moving mesh methods. While these methods reduce the truncation error, none of them eliminate it entirely, and therefore formally solutions will still violate Galilean invariance at the level of the truncation error.