Documentation/UserGuide/Reconstruction

Reconstruction is the method by which the cell-centered, volume averaged values of conserved quantities are interpolated to cell faces, in order to calculate the left- and right-states needed to compute fluxes using a Riemann solver. For example, the figure below shows piecewise linear reconstruction at the interface located between cells i-1 and i.

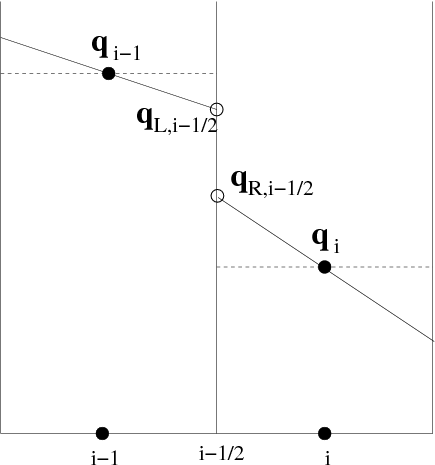
Several different reconstruction algorithms are implemented in Athena, see section 4.2 of the ApJS Method Paper for more details.

Reconstruction is one of the most important algorithmic elements of a Godunov code. The accuracy of any application will depend on which reconstruction algorithm is used. Third order reconstruction is recommended for all applications using Athena.

Each of the different reconstruction algorithms are implemented in different files in the directory /athena/src/reconstruction/

First-order (piecewise constant) reconstruction

Configure with:

    % configure --with-order=1

Very diffusive. Useful for testing, or when all other reconstruction methods fail, but should never be used for applications.

Second-order (piecewise linear) reconstruction (default)

To use slope-limiting in the characteristic variables, configure with

    % configure --with-order=2

To use slope-limiting in the primitive variables, configure with

    % configure --with-order=2p

Either of these options dramatically reduces the numerical diffusion of the reconstruction algorithm compared to the first-order method. Either can be used for applications, although third-order is generally better. Especially useful for problems where a little more spatial diffusion is actually desirable.

Third-order (piecewise parabolic) reconstruction

To use slope-limiting in the characteristic variables, configure with

    % configure --with-order=3

To use slope-limiting in the primitive variables, configure with

    % configure --with-order=3p

The most complicated, and most accurate, reconstruction algorithm in Athena. Formally, other parts of the algorithm (e.g. the Integrators) limit the overall accuracy to second-order, but using third-order reconstruction can noticably reduce errors (see Fig. 33 of the ApJS Method Paper).