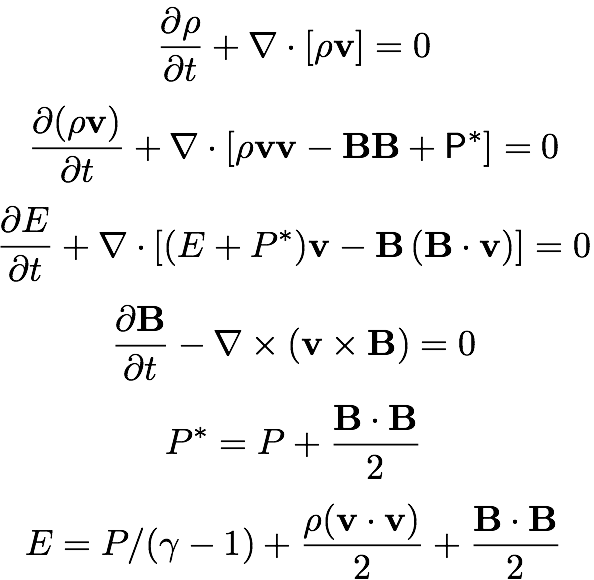Equations Solved
Ideal MHD
In its default configuration, Athena solves the equations of compressible, adiabatic, inviscid, ideal magnetohydrodynamics (MHD).
where ρ is the mass density, $v$ the velocity, $E$ the total energy density, $B$ the magnetic field, $P$ the gas pressure, and $\gamma$ the adiabatic index (ratio of specific heats). These equations are written using units in which the magnetic permeability $\mu=1$. Note there is no microscopic dissipation of any kind (viscosity, resistivity, or conduction) in the default configuration.
Hydrodynamics
By configuring the code for hydrodynamics, using
configure --with-gas=hydro
Athena will solve the Euler equations, i.e. the above system with the fourth (the induction) equation, and all terms that depend on the magnetic field $B$, dropped.
Isothermal Hydrodynamics and MHD
By configuring the code for an isothermal equation of state, using
configure --with-eos=isothermal
Athena will solve the above system with the third (the energy) and the last equations dropped, and using a gas pressure $P$ given by an isothermal equation of state $P = C^2\rho$, where $C$ is the isothermal sound speed.
Additional Physics
Athena includes options for a wide range of additional physics, represented by the following system of equations:
In the above, $C_i\ i=1,…,N$ are the mass fractions of $N$ passive scalars. This allows for evolving fluids composed of multiple species, e.g. neutrals and ions.
$\phi$ and $\varphi$ are the gravitational potentials due to the fluid (self-gravity) and/or a fixed external mass, respectively. The former is given by a solution of Poisson’s equation. Stresses due to self-gravity are added through the gravitational stress tensor $G$. The static gravitational potential $\varphi$ can be set to any function of position.
$\Pi$ is the viscous stress tensor, which contains both isotropic and anisotropic components, controlled by the coefficients $\nu_0$ and $\nu_{||}$ respectively. In the anisotropic case, the viscous flux is confined to be parallel to the magnetic field lines.
$Q$ is the heat flux, which contains both isotropic and anisotropic components, controlled by the coefficients $\kappa_0$ and $\kappa_{||}$ respectively. In the anisotropic case, the heat flux is confined to be parallel to the magnetic field lines.
$H$ is a per particle external heating rate, while $\Lambda$ is the per-particle cooling rate due to optically-thin radiation. Both can be set to arbitrary functions.
The induction equation includes a variety of non-ideal MHD effects, including Ohmic dissipation (controlled by the resistivity $\eta$), the Hall effect (controlled by $\eta_H$) and ambipolar diffusion (controlled by $\eta_{AD}$).