Because Tristan v2 uses adjustable number of ghost zones per each MPI subdomain it is fairly easy to implement any high order Maxwell solver schemes or different particle shape functions. However, in its most basic version we use the simplest schemes. Recommended minimum number of ghost cells is --NGHOSTS=3, but keep in mind that the performance may vary with different number of ghost cells depending on the particular setup. We focus on the main loop with the correct ordering of operations in the other section. In this section we describe the numerical aspects of each of the substeps.
Field solver #
Electric and magnetic fields are staggered spatially in the so-called Yee mesh pattern. Magnetic field is also staggered temporally, to ensure all the derivatives are time-centered. This means at any given timestep $n$ in a given cell $i$, $j$, $k$ we have the following components of the electromagnetic field and the current density:
\begin{equation*} \begin{aligned} &e_{x\,(i,j-1/2,\,k-1/2)}^{(n)},&\,&e_{y\,(i-1/2,\,j,\,k-1/2)}^{(n)},&\,&e_{z\,(i-1/2,\,j-1/2,\,k)}^{(n)}, \\ &b_{x\,(i-1/2,\,j,\,k)}^{(n-1/2)},&\,&b_{y\,(i,\,j-1/2,\,k)}^{(n-1/2)},&\,&b_{z\,(i,\,j,\,k-1/2)}^{(n-1/2)}, \\ &j_{x\,(i,\,j-1/2,\,k-1/2)}^{(n)},&\,&j_{y\,(i-1/2,\,j,\,k-1/2)}^{(n)},&\,&j_{z\,(i-1/2,\,j-1/2,\,k)}^{(n)}, \end{aligned} \end{equation*}
where $(i,j,k)$ corresponds to the center of the cell, and $(n)$ is the beginning of the timestep.
Maxwell solver itself consists of three separate substeps. Faraday’s law over half timestep $\Delta t/2$ (called twice):
\begin{equation*} \begin{aligned} \frac{\bm{B}^{(n)} - \bm{B}^{(n-1/2)}}{\Delta t/2} &= -\tilde{c}\nabla\times \bm{E}^{(n)},\,\text{and}\\ \frac{\bm{B}^{(n+1/2)} - \bm{B}^{(n)}}{\Delta t/2} &= -\tilde{c}\nabla\times \bm{E}^{(n)}. \end{aligned} \end{equation*}
The Ampere’s law over the full timestep $\Delta t$:
\begin{equation*} \frac{\bm{\tilde{E}}^{(n+1)} - \bm{E}^{(n)}}{\Delta t} = \tilde{c}\nabla\times \bm{B}^{(n+1/2)}. \end{equation*}
And the correction to the Ampere’s law from the deposited currents:
\begin{equation*} \bm{E}^{(n+1)} = \bm{\tilde{E}}^{(n+1)} - \bm{j}^{(n)}. \end{equation*}
This is sometimes called a leap-frog approach; intermediate value of $\bm{B}^{(n)}$ is used for particle push. All the procedure is shown in the animation below.
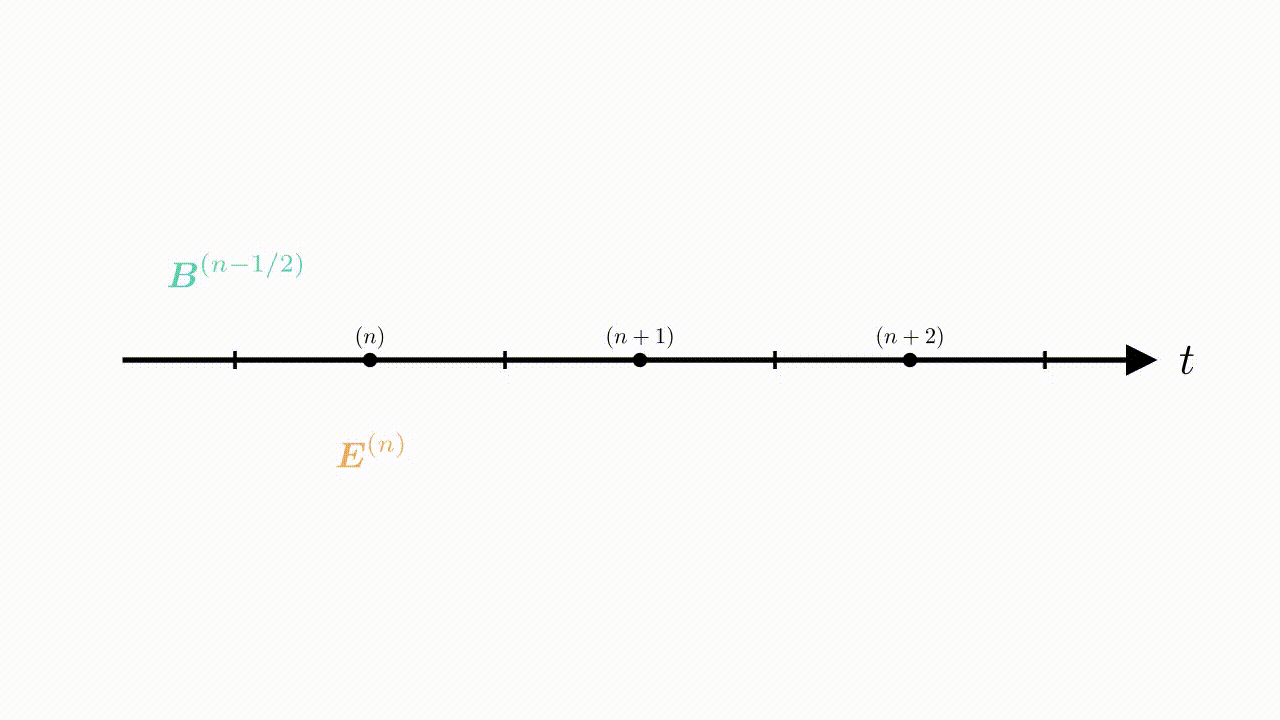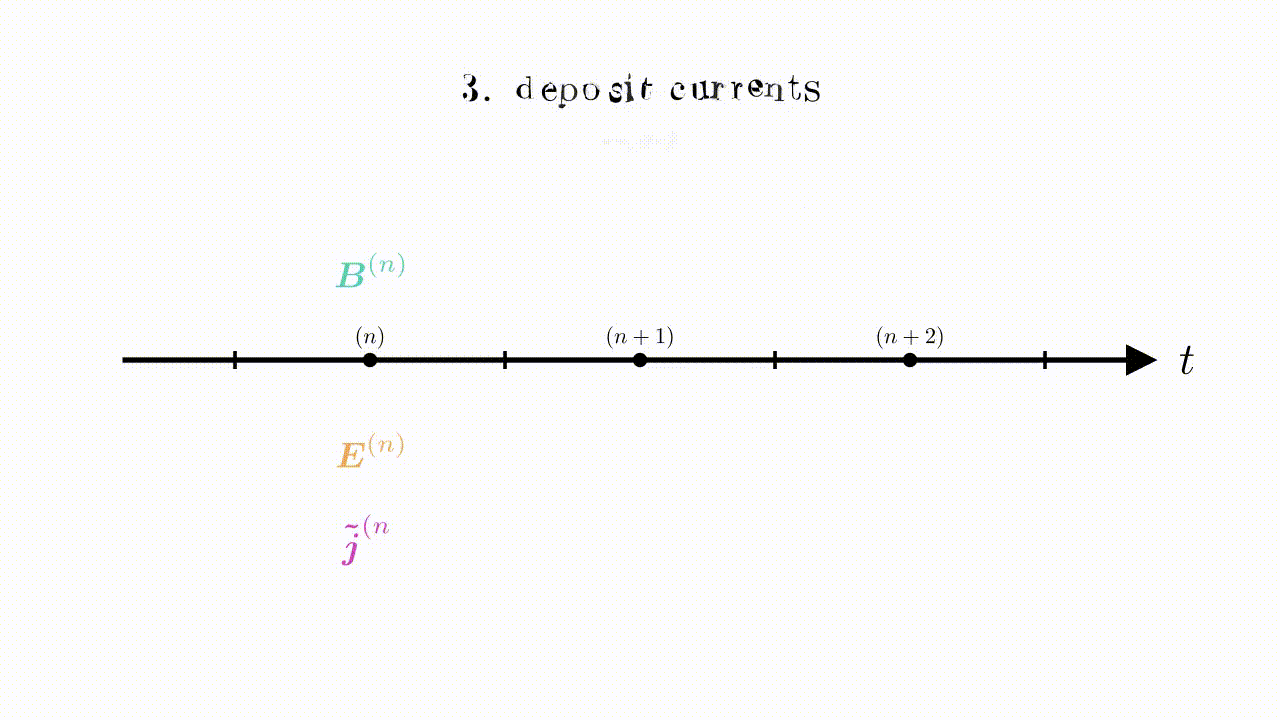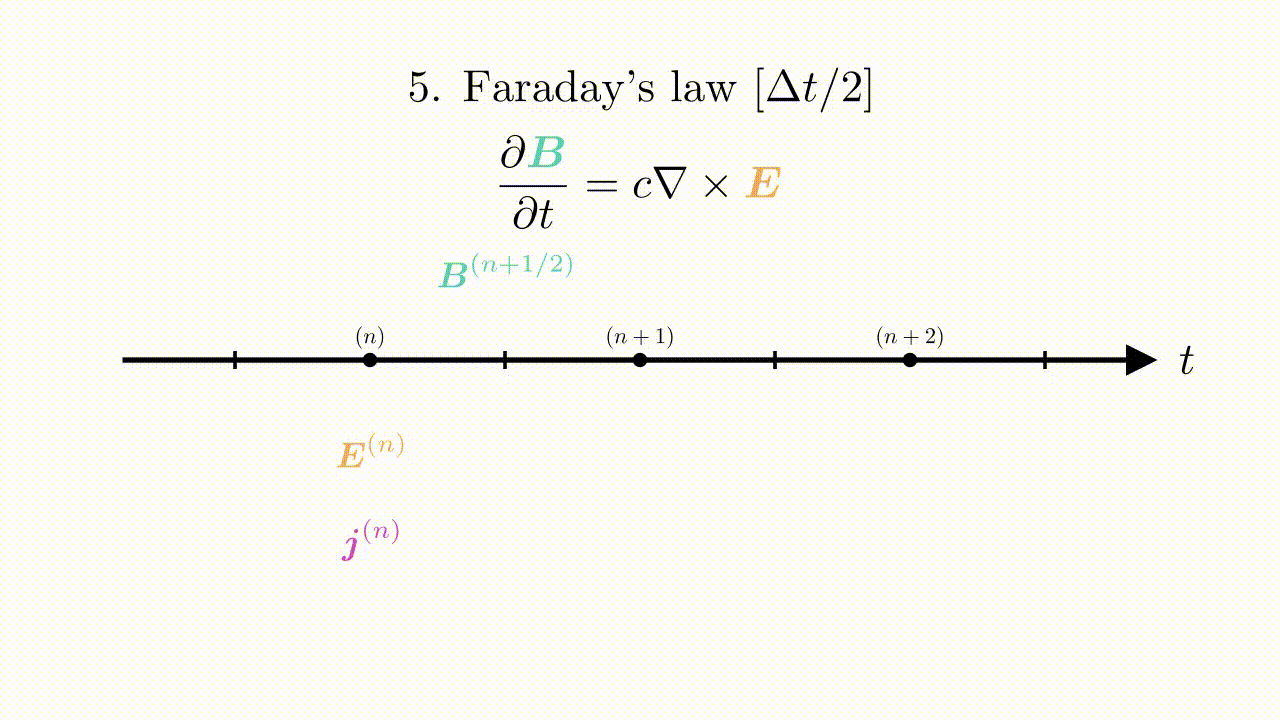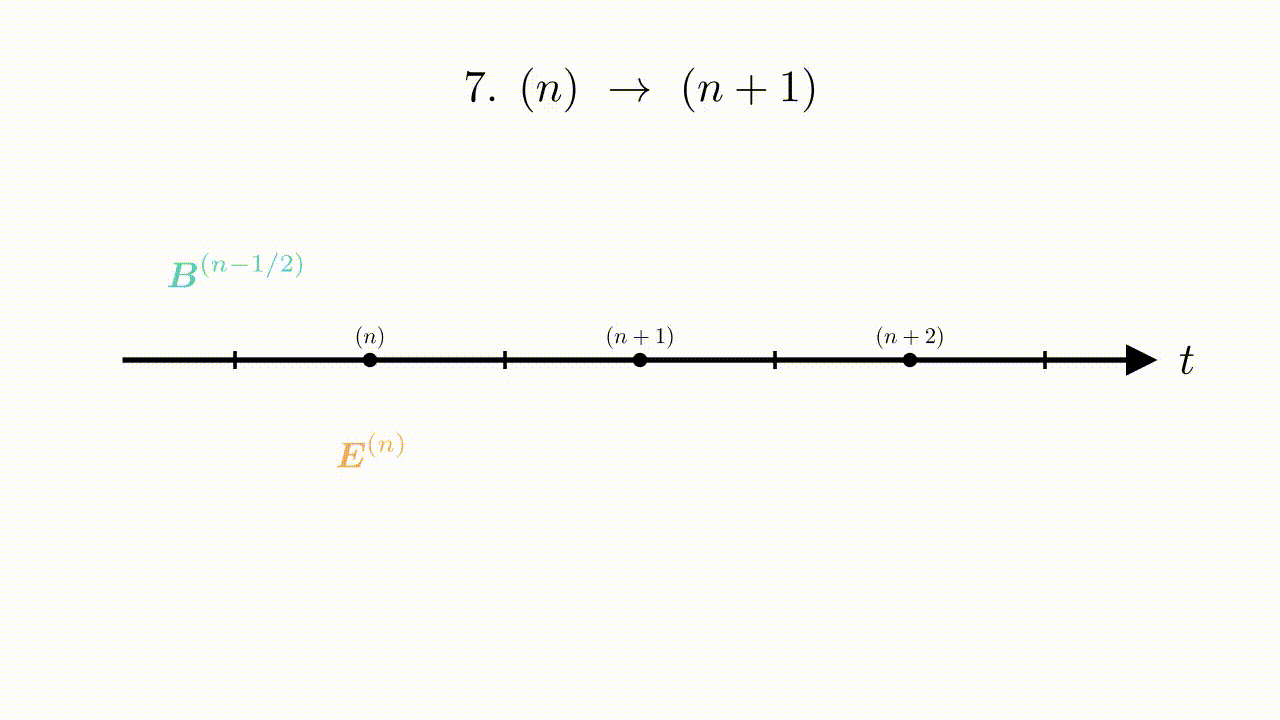
Notice that we use a corrected speed of light, $\tilde{c}\approx 1.025 c$, to ensure particles never travel faster than the vacuum electromagnetic waves. This is a hack, but it seems to work nice nevertheless.
Particle pusher #
Guiding center approximation #
The GCA algorithm is an alternative particle pusher which may be used when the Larmor radius is critically underresolved. It relies on the conservation of adiabatic invariant, while evolving the parallel (w.r.t. the local magnetic field) component of the velocity according to the $E_\parallel$. To enable GCA one has to compile the code with the -gca flag. Keep in mind that the curvature term is still not implemented, so the current version of the GCA algorithm might be unusable for cases where the curvature drift is important.
This algorithm is only used in hybrid with the default Boris pusher, with the GCA only pushing the particles for which the electric field and the gyroradius are small: $E < f B$ and $\rho_L < \rho_{\rm crit}$ (in cells). Parameters $f$ and $\rho_{\rm crit}$ are configured in the input:
<algorithm>
...
gca_rhoL = 1 # critical larmor radius at which GCA kicks in
gca_EoverB = 1 # critical E/B at which GCA kicks in
One can also enable/disable GCA for certain particle species (defaults to .true. if particles are charged and the -gca flag is enabled):
<particles>
...
gca1 = 1 # use GCA for species #1
gca2 = 0 # never use GCA for species #2