Basics and Primer

• Basics

• Primer

  • Simple Configurations

  • More Elaborate Configurations

  • Dynamics of Execution

  • Control

  • Parameters

  • Displaying and Logging Values

  • Learning

  • Customization

Basics

Overview

PsyNeuLink models are made up of Components and Compositions: Components are objects that perform a specific function, and Compositions are used to combine Components into a model. There are two primary kinds of Components: Mechanisms and Projections. For those familiar with block modeling systems, Mechanisms are the “blocks” in PsyNeuLink, and Projections are the “links”. Mechanisms take inputs, use a function to process them in some way, and generate outputs that can be sent to other Mechanisms. Projections allow the output of one Mechanism to be transmitted to another. Compositions combine these Components into pathways that constitute a computational graph, in which the Mechanisms are nodes and Projections are directed edges. Compositions can also be nodes, so that one Composition can be nested inside another to create more complex, hierarchical models (e.g., of circuits or pathways within a larger system-level model). A Scheduler coordinates the execution of all of the Components in a model. By default, it executes them in the order determined by the Projections among the Mechanisms and/or nested Compositions. However, individual Components can be assigned one or more pre-specified or customized Conditions to handle more complex structures, such as feedback pathways, and/or the execution of Components at different time scales (e.g., a recurrent network that needs time to settle before passing information to a decision layer).

Mechanisms and Projections

Mechanisms and Projections fall into two broad categories: ProcessingMechanisms directly transmit and possibly transform information, and are linked by PathwayProjections that transmit the information between them. ModulatoryMechanisms <ModulatoryMechanism>` *modify or modulate the transmission and transformation of information, by way of ModulatoryProjections to the Components they modulate. PsyNeuLink provides a library of Components of each type. For example, there is a variety of ProcessingMechanisms that can be used to transform, integrate, and evaluate information in various ways (e.g., to implement layers of a feedforward or recurrent neural network, or a drift diffusion decision process); and there are ModulatoryMechanisms, including ControlMechanisms that can be used modulate the functioning of ProcessingMechanisms, and LearningMechanisms that can be used to modify Projections, respectively. The function of a Mechanism defines the operation it carries out. PsyNeuLink provides a rich library of mathematical, statistical and matrix manipulation functions. However, a Mechanism can also be assigned any Python function that is consistent with that Mechanism’s type (see Customization). Since Mechanisms can implement virtually any function, Projections ensure that they can “communicate” with each other seamlessly.

Together, these elements allow PsyNeuLink to implement and integrate processes of different types, levels of analysis, and/or time scales of operation, composing them into a coherent system. This affords modelers the flexibility to commit each part of their model to a form of processing and/or level of analysis that is appropriate for that part, while providing the opportunity to test and explore how they interact with one another at the level of the entire system. The figure below provides an example of the kinds of elements available in PsyNeuLink, and some that are planned for future inclusion. The Quick Reference provides a more detailed overview of PsyNeuLink objects and its other facilities. In the sections that follow, the Primer provides some examples of how these are used to construct models in PsyNeuLink.

PsyNeuLink Environment. Full-colored items are examples of currently implemented elements; dimmed items are examples of elements planned for future implementation.

Primer

The examples below are intended to provide quick illustrations of some of PsyNeuLink’s basic and more advanced capabilities. They assume some experience with computational modeling and/or relevant background knowledge. The tutorial provides additional introductory material for those who are newer to computational modeling, as well as a more detailed and comprehensive introduction to the use of PsyNeuLink.

Simple Configurations

Mechanisms can be executed on their own (to gain familiarity with their operation, or for use in other Python applications), or linked together and run in a Composition to implement part of, or an entire model. Linking Mechanisms for execution can be as simple as creating them and then assiging them to a Composition in a list – PsyNeuLink provides the necessary Projections that connect each to the next one in the list, making reasonable assumptions about their connectivity. The following example creates a 3-layered 5-2-5 neural network encoder network, the first layer of which takes an an array of length 5 as its input, and uses a Linear function (the default for a ProcessingMechanism), and the other two of which take 1d arrays of the specified sizes and use a Logistic function:

# Construct the Mechanisms:
input_layer = ProcessingMechanism(input_shapes=5, name='Input')
hidden_layer = ProcessingMechanism(input_shapes=2, function=Logistic, name='hidden')
output_layer = ProcessingMechanism(input_shapes=5, function=Logistic, name='output')

# Construct the Composition:
my_encoder = Composition(pathways=[[input_layer, hidden_layer, output_layer]])

Each of the Mechanisms can be executed individually, by simply calling its execute method with an appropriately-sized input array, for example:

output_layer.execute([0, 2.5, 10.9, 2, 7.6])
>> array([[0.5, 0.92414182, 0.99998154, 0.88079708, 0.9994998 ]])

The Composition connects the Mechanisms into a pathway that form a graph, which can be shown using its show_graph method:

Composition Graph. Representation of the graph of the simple Composition in the example above. Note that the Input Mechanism for the Composition is colored green (to designate it is an INPUT node), and its output Mechanism is colored Red (to designate it at a OUTPUT node).

As the name of the show_graph() method suggests, Compositions are represented in PsyNeuLink as graphs, using a standard dependency dictionary format, so that they can also be submitted to other graph theoretic packages for display and/or analysis (such as NetworkX and igraph). They can also be exported as a JSON file, in a format that is currently being developed for the exchange of computational models in neuroscience and psychology (see json)

The Composition can be run by calling its run method, with an input array appropriately sized for the first Mechanism in the pathway (in this case, the input_layer):

my_encoder.run([1, 4.7, 3.2, 6, 2])
[array([0.88079707, 0.88079707, 0.88079707, 0.88079707, 0.88079707])]

The order in which Mechanisms appear in the list of the pathways argument of the Composition’s constructor determines their order in the pathway. More complicated arrangements can be created by using one of the Compositions pathway addition methods, by adding nodes individually using a Composition’s add_nodes method, and/or by creating intersecting pathways, as shown in some of the examples further below.

PsyNeuLink picks sensible defaults when necessary Components are not specified. In the example above no Projections were actually specified, so PsyNeuLink automatically created the appropriate types (in this case, MappingProjections), and sized them appropriately to connect each pair of Mechanisms. Each Projection has a matrix parameter that weights the connections between the elements of the output of its sender and those of the input to its receiver. Here, the default is to use a FULL_CONNECTIVITY_MATRIX, that connects every element of the sender’s array to every element of the receiver’s array with a weight of 1. However, it is easy to specify a Projection explicitly, including its matrix, simply by inserting them in between the Mechanisms in the pathway:

my_projection = MappingProjection(matrix=(.2 * np.random.rand(2, 5)) - .1))
my_encoder = Composition()
my_encoder.add_linear_processing_pathway([input_layer, my_projection, hidden_layer, output_layer])

The first line above creates a Projection with a 2x5 matrix of random weights constrained to be between -.1 and +.1, which is then inserted in the pathway between the input_layer and hiddeen_layer. Note that here, one of the Composition’s pathway addition methods is used to create the pathway, as an alternative to specifying it in the pathways argument of the constructor (as shown in the initial example). The Projection’s matrix itself could also have been inserted directly, as follows:

my_encoder.add_linear_processing_pathway([input_layer, (.2 * np.random.rand(2, 5)) - .1)), hidden_layer, output_layer])

PsyNeuLink knows to create a MappingProjection using the matrix. PsyNeuLink is also flexible. For example, a recurrent Projection from the output_layer back to the hidden_layer can be added simply by adding another entry to the pathway:

my_encoder.add_linear_processing_pathway([input_layer, hidden_layer, output_layer, hidden_layer])

This tells PsyNeuLink to create a Projection from the output_layer back to the hidden_layer. The same could have also been accomplished by explicitly creating the recurrent connection:

my_encoder.add_linear_processing_pathway([input_layer, hidden_layer, output_layer])
recurent_projection = MappingProjection(sender=output_layer,
                  receiver=hidden_layer)
my_encoder.add_projection(recurent_projection)

More Elaborate Configurations

Configuring more complex models is also straightforward. For example, the script below implements a model of the Stroop task by creating two feedforward neural network pathways – one for color naming and another for word reading – as well as a corresponding pair of pathways that determine which of those to perform based on a task instruction. These all converge on a common output mechanism that projects to a drift diffusion (DDM) decision mechanism responsible for determining the response:

# Construct the color naming pathway:
color_input = ProcessingMechanism(name='COLOR INPUT', input_shapes=2) # note: default function is Linear
color_input_to_hidden_wts = np.array([[2, -2], [-2, 2]])
color_hidden = ProcessingMechanism(name='COLOR HIDDEN', input_shapes=2, function=Logistic(bias=-4))
color_hidden_to_output_wts = np.array([[2, -2], [-2, 2]])
output = ProcessingMechanism(name='OUTPUT', input_shapes=2 , function=Logistic)
color_pathway = [color_input, color_input_to_hidden_wts, color_hidden, color_hidden_to_output_wts, output]

# Construct the word reading pathway (using the same output_layer)
word_input = ProcessingMechanism(name='WORD INPUT', input_shapes=2)
word_input_to_hidden_wts = np.array([[3, -3], [-3, 3]])
word_hidden = ProcessingMechanism(name='WORD HIDDEN', input_shapes=2, function=Logistic(bias=-4))
word_hidden_to_output_wts = np.array([[3, -3], [-3, 3]])
word_pathway = [word_input, word_input_to_hidden_wts, word_hidden, word_hidden_to_output_wts, output]

# Construct the task specification pathways
task_input = ProcessingMechanism(name='TASK INPUT', input_shapes=2)
task_color_wts = np.array([[4,4],[0,0]])
task_word_wts = np.array([[0,0],[4,4]])
task_color_pathway = [task_input, task_color_wts, color_hidden]
task_word_pathway = [task_input, task_word_wts, word_hidden]

# Construct the decision pathway:
decision = DDM(name='DECISION', input_format=ARRAY)
decision_pathway = [output, decision]

# Construct the Composition:
Stroop_model = Composition(name='Stroop Model')
Stroop_model.add_linear_processing_pathway(color_pathway)
Stroop_model.add_linear_processing_pathway(word_pathway)
Stroop_model.add_linear_processing_pathway(task_color_pathway)
Stroop_model.add_linear_processing_pathway(task_word_pathway)
Stroop_model.add_linear_processing_pathway(decision_pathway)

This is a simplified version the model described in Cohen et al. (1990) .

The figure belows shows the model using the Composition’s show_graph method.

Stroop Model. Representation of the Composition in the example above.

Running the model is as simple as generating some inputs and then providing them to the run method. Inputs are specified in a dictionary, with one entry for each of the Composition’s INPUT Mechanisms; each entry contains a list of the inputs for the specified Mechanism, one for each trial to be run. The following defines two stimuli to use as the color and word inputs (red and green), and two for use as the task input (color and word), and then uses them to run the model for a color naming congruent trial, followed by a color naming incongruent trial:

red =   [1,0]
green = [0,1]
word =  [0,1]
color = [1,0]
                                   # Trial 1  Trial 2
Stroop_model.run(inputs={color_input:[red,     red   ],
                         word_input: [red,     green ],
                         task_input: [color,   color ]})
print(Stroop_model.results)
>> [[array([1.]), array([2.80488344])], [array([1.]), array([3.94471513])]]

When a Composition is run, its results attribute stores the values of its OUTPUT Mechanisms at the end of each trial. In this case, the DDM Mechanism is the only OUTPUT Mechanism, and it has two output values by default: the outcome of the decision (1 or -1, in this case corresponding to red or green), and the estimated mean decision time for the decision (in seconds). So, the value returned by the results attribute is a 3d array containing two 2d arrays, each of which has the two outputs of the DDM for each trial (notice that the estimated response time for the second, incongruent trial was significantly longer than for the first, congruent trial; note also that, on some executions it might return -1 as the response in the second trials since, by default, the function used for the decision process has a non-zero noise term).

Dynamics of Execution

One of the most powerful features of PsyNeuLink is its ability to simulate models with Components that execute at different time scales. By default, each Mechanism executes once per pass through the Composition, in the order determined by the projections between them (and shown in the show_graph method. In the Stroop_model above, the decision Mechanism executes once per pass, just after the ouput Mechanism. The decision Mechanism is a DDM. This uses DriftDiffusionAnalytical as its default function, which computes an analytic solution to the distribution of responses using the DDM integration process, and returns both the probability of crossing a specified threshold), and the mean crossing time. However, it is also possible to simulate the dynamics of the integration process. This can be done by assigning DriftDiffusionIntegrator as the Mechanism’s function and, in the call to the Composition’s run method, specifying that a trial terminates only when the decision Mechanism has completed its execution, as follows:

# Modify consruction of decision Mechanism:
decision = DDM(name='DECISION',
               input_format=ARRAY,
               reset_stateful_function_when=AtTrialStart(),
               function=DriftDiffusionIntegrator(noise=0.5, threshold=20)
               )
Stroop_model.run(inputs={color_input:red, word_input:green, task_input:color},
                 termination_processing={TimeScale.TRIAL: WhenFinished(decision)}
                 )
print (Stroop_model.results)
>> [[array([[20.]]), array([[126.]])]]

The output is now the result of the DriftDiffusionIntegrator, which is the value of the decision variable when it crosses threshold (which is, by definition, equal to either the postive or negative value of the threshold attribute), and the number of executions it took to do so. Since the decision Mechanism is the last (TERMINAL) Mechanism of the Composition, it is also its OUTPUT Mechanism. Therefore, its output is recorded in the results attribute of the Stroop model, as shown above (note: because there is noise in the integration process, running the model several times produces varying response times).

This version of the model includes Mechanisms that execute over different time-scales. The ProcessingMechanisms completed their computations in a single execution, whereas the DDM took many executions to complete its computation. In this case, the coordination of time scales was straightforward, since the DDM was the last Mechanism in the Composition: the ProcessingMechanisms in each pathway executed in sequence, ending in the DDM which executed until it was complete. PsyNeuLink’s Scheduler can be used to implement more complicated dependencies among Mechanisms, by creating one or more Conditions for execution of those Mechanisms and assigning those to the Composition’s Scheduler. Conditions can specify the behavior of a Mechanism on its own (e.g., how many times it should be executed in each trial), its behavior relative to one or more other Components (e.g., how many times it should wait for another Mechanism to execute before it does so), or even arbitrary functions (e.g., a convergence criterion for the settling of a recurrent network). For example, the following implements a version of the model above that uses a leaky competing accumulator (LCAMechanism) for the task Mechanism. The latter settles for a specified number of executions before the color and word hidden layers execute, simulating a situation in which the task instruction is processed before processing the color or word stimuli:

# Modify consruction of task Mechanism:
task = LCAMechanism(name='TASK', input_shapes=2)

# Assign conditions to scheduler:
Stroop_model.scheduler.add_condition(color_hidden, EveryNExecutions(task, 10))
Stroop_model.scheduler.add_condition(word_hidden, EveryNExecutions(task, 10))

# Run with scheduler:
Stroop_model.run(inputs={color_input:red, word_input:green, task_input:color})
print (Stroop_model.results)
>>[[array([[20.]]), array([[42.]])]]

In the example above, the color_hidden and word_hidden Mechanisms both wait to execute until the task Mechanism has executed 100 times. They could also each have been made to wait different numbers of times; in that case, since the output Mechanism depends on both them, it would have waited until they had both executed before doing so itself. This example also imposes a fixed “setting time” (100 executions) on the task Mechanism. However, it could also be allowed to settle until it reaches some criterion. For example, the color_hidden and word_hidden can be configured to wait until the value of the task Mechanism “converges”, by changing the conditions for execution of the color_hidden and task_hidden Mechanism’s to depend on a function, as follows:

# Define a function that detects when the a Mechanism's value has converged, such that the change in all of the
elements of its value attribute from the last execution (given by its delta attribute) falls below ``epsilon``

def converge(mech, thresh):
    return all(abs(v) <= thresh for v in mech.delta)

# Add Conditions to the ``color_hidden`` and ``word_hidden`` Mechanisms that depend on the converge function:
epsilon = 0.01
Stroop_model.scheduler.add_condition(color_hidden, When(converge, task, epsilon)))
Stroop_model.scheduler.add_condition(word_hidden, When(converge, task, epsilon)))

PsyNeuLink provides a rich set of pre-defined Conditions (such as When in the examples above), but Conditions can also be constructed using any Python function. Together, these can be combined to construct virtually any schedule of execution that is logically possible.

Control

Another distinctive feature of PsyNeuLink is the ability to easily create models that include control; that is, Mechanisms that can evaluate the output of other Mechanisms (or nested Compositions), and use this to regulate the processing of those Mechanisms. For example, modifications of the Stroop_model shown below allow it to monitor conflict in the output Mechanism on each trial, and use that to regulate the gain of the task Mechanism:

# Construct control mechanism
control = ControlMechanism(name='CONTROL',
                           objective_mechanism=ObjectiveMechanism(name='Conflict Monitor',
                                                                  monitor=output,
                                                                  function=Energy(input_shapes=2,
                                                                                  matrix=[[0,-2.5],[-2.5,0]])),
                           default_allocation=[0.5],
                           control_signals=[(GAIN, task)])

# Construct the Composition using the control Mechanism as its controller:
Stroop_model = Composition(name='Stroop Model', controller=control)

# Print statement called by run method (below), that show state of Components after each trial
np.set_printoptions(precision=2)
global t
t = 0
def print_after():
    global t
    print(f'\nEnd of trial {t}:')
    print(f'\t\t\t\tcolor  word')
    print(f'\ttask:\t\t{task.value[0]}')
    print(f'\ttask gain:\t   {task.parameter_ports[GAIN].value}')
    print(f'\t\t\t\tred   green')
    print(f'\toutput:\t\t{output.value[0]}')
    print(f'\tdecision:\t{decision.value[0]}{decision.value[1]}')
    print(f'\tconflict:\t  {control.objective_mechanism.value[0]}')
    t += 1

# Set up run and then execute it
task.initial_value = [0.5,0.5]         # Assign "neutral" starting point for task units on each trial
task.reset_stateful_function_when=AtTrialStart()  # Reset task units at beginning of each trial
num_trials = 4
stimuli = {color_input:[red]*num_trials,
           word_input:[green]*num_trials,
           task_input:[color]*num_trials}
Stroop_model.run(inputs=stimuli, call_after_trial=print_after)

This example takes advantage of several additional features of PsyNeuLink, including its ability to automate certain forms of construction, and perform specified operations at various points during execution (e.g., reset variables and call user-defined functions). For example, the constructor for the ControlMechanism can be used to specify how control should be configured, and automates the process of implementing it: the objective_mechanism argument specifies the construction of an ObjectiveMechanism for the ControlMechanism that provides its input, and the control_signals argument specifies the parameters of the Mechanisms it should regulate and constructs the ControlProjections that implement this. Furthermore, the constructor for the ObjectiveMechanism used in the objective_mechanism argument specifies that it should monitor the value of the output Mechanism, and use the Energy Function to evaluate it. PsyNeuLink automatically constructs the MappingProjections from output to the ObjectiveMechanism, and from the latter to the ControlMechanism. The latter is then added to the Stroop_model as its controller in its constructor. The result is shown in the figure below, using the show_controller option of the Composition’s show_graph method:

Stroop Model with Controller. Representation of the Composition with the control Mechanism added, generated by a call to Stroop_model.show_graph(show_controller).

The task Mechanism is configured to reset at the beginning of each trial, and the call_after_trial argument of the Composition’s run method is used to print Mechanism values at the end of each trial (see below).

When the Composition executes, the Objective Mechanism receives the output of the output Mechanism, and uses the Energy function assigned to it to compute conflict in the output Mechanism (i.e., the degree of co-activity of the red and green values). The result passed to the control Mechanism, which uses it to set the gain of the task Mechanism’s Logistic function. The task Mechanism is configured to reset at the beginning of each trial; and,since the control Mechanism was assigned as the Composition’s controller, it executes at the end of each trial after all of the other Mechanisms in the Composition have executed, which has its effects on the task Mechanism the next time it executes (i.e., on the next trial; a Composition’s controller can also be configured to execute at the start of a trial). Finally, the call_after_trial argument of the Composition’s run method is used to print Mechanism values at the end of each trial. The animate argument of the run method can be used to generate an animation of the Composition’s execution, as shown below:

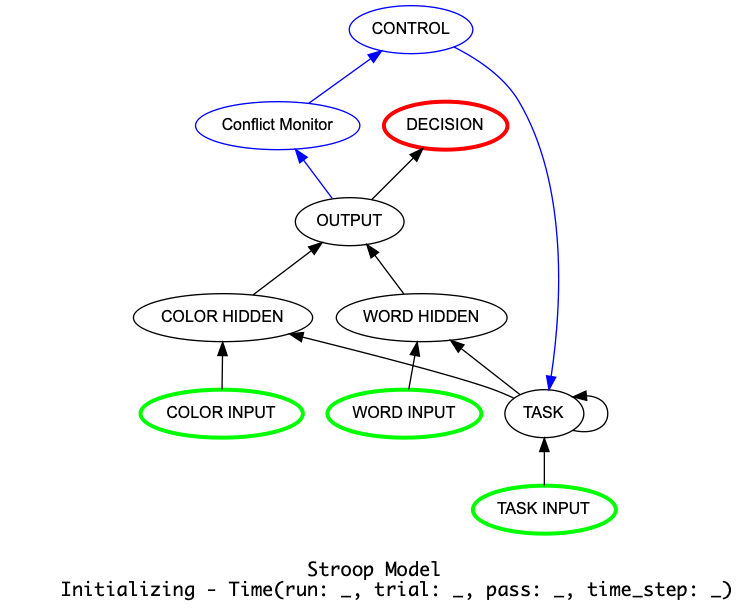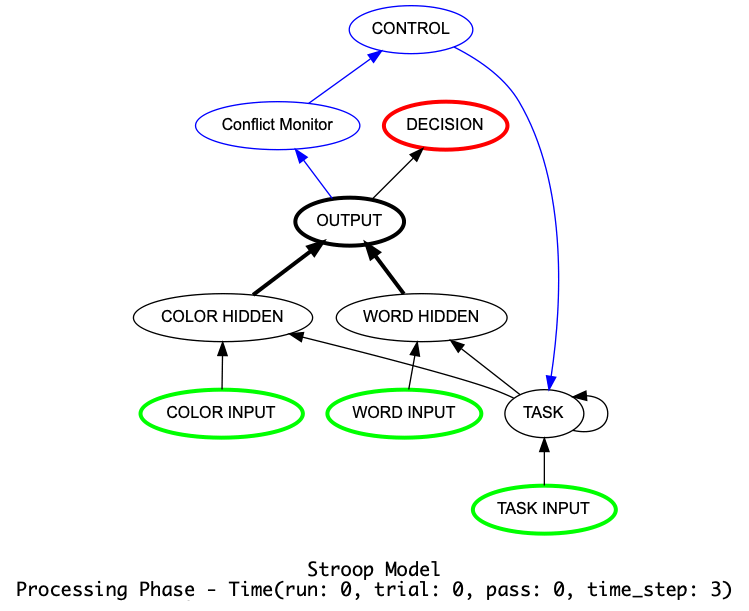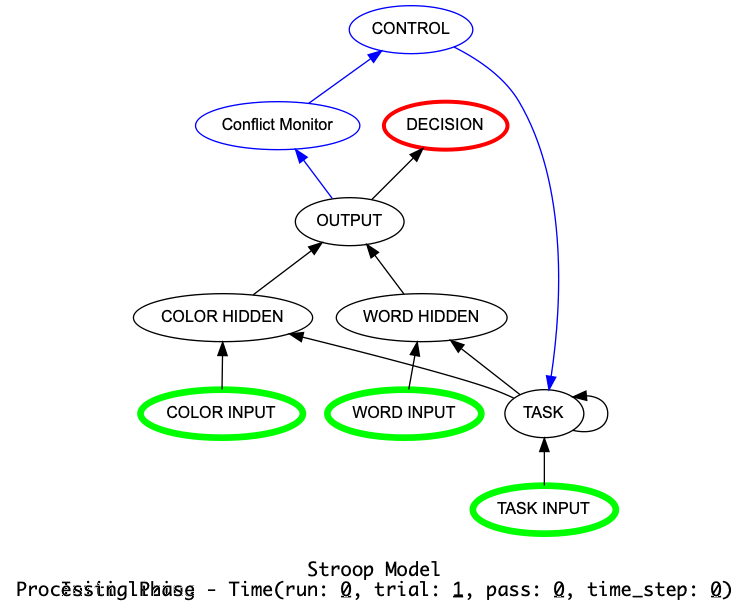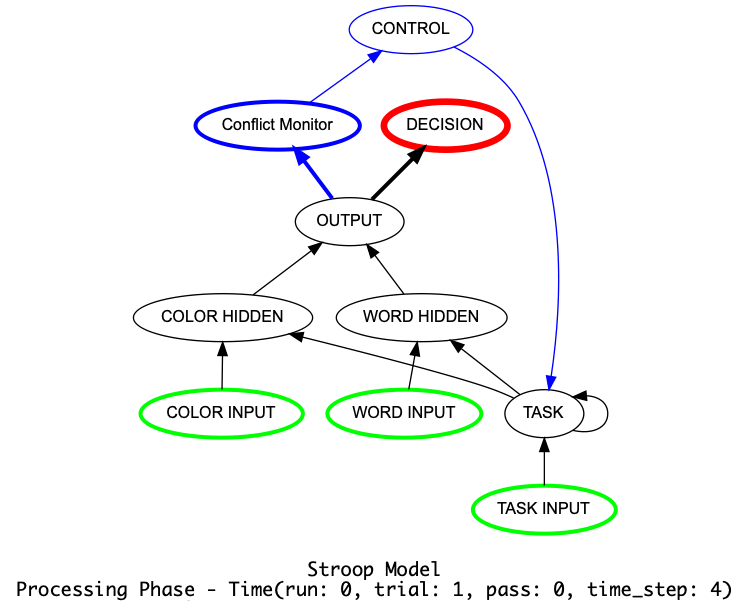
Animation of Stroop Model with Controller. Generated by a call to Stroop_model.show_graph(show_controller) with ``animate={"show_controller":True} in call to the run.

Running it for four trials produces the following output:

.. _Stroop_model_output:

End of trial 0:
                color  word
    task:           [ 0.67  0.51]
    task gain:         [ 0.5]
                red   green
    output:         [ 0.28  0.72]
    decision:       [-1.][ 2.36]
    conflict:         [ 0.51]

End of trial 1:
                color  word
    task:           [ 0.81  0.4 ]
    task gain:         [ 0.51]
                red   green
    output:         [ 0.38  0.62]
    decision:       [-1.][ 3.33]
    conflict:         [ 0.59]

End of trial 2:
                color  word
    task:           [ 0.97  0.19]
    task gain:         [ 0.59]
                red   green
    output:         [ 0.55  0.45]
    decision:       [ 1.][ 3.97]
    conflict:         [ 0.62]

End of trial 3:
                color  word
    task:           [ 1.    0.04]
    task gain:         [ 0.62]
                red   green
    output:         [ 0.65  0.35]
    decision:       [ 1.][ 2.95]
    conflict:         [ 0.57]

Notice that initially, because control starts out relatively low (default_allocation=[0.5]), the representation of the instruction in the task Mechanism (color = [1,0]) is relatively weak ([0.67, 0.51]). As a result, the model generates the incorrect response to the incongrent stimulus([-1] = green, rather than [1] = red), due to the stronger weights of the Projections in the word_pathway. However, beacuse this is associated with a moderate amount of conflict ([0.51]), control is increased on the next trial, which in turn increases the gain of the task Mechanism, stengthening its representation of the instruction so that it eventually fully activates the color task and generates the correct response. A more elaborate example of this model can be found at Conflict Monitoring and Cognitive Control (Botvinick et al., 2001). More complicated forms of control are also possible, for example, ones that run internal simulations to optimize the amount of control to optimize some criterion (e.g,. maximize the expected value of control (see XXX EVC script), or to implement model-based learning (see XXX LVOC script). .. FIX: ADD LINKS TO SCRIPTS ABOVE

Parameters

Every Component has a set of parameters that determine how the Component operates, or that contain information about the state of its operation. For example, every Component has a value parameter that stores the result of the Component’s function after it has executed. (Note here the difference in the generic use of the term “value” to designate the quantity assigned to a parameter, and its use as the name of a particular parameter of a Component.) Although parameters are attributes of a Component, and can be accessed like any other Python attribute (as described below), they are actually instances of a special Parameters class that supports a number of important features. These include the ability to simultaneously have different values in different contexts (often referred to as "statefulness"), the ability to keep a record of previous values, and the ability to be modulated by other Components in PsyNeuLink. These features are supported by methods on the Parameter class, as described below.

Accessing Parameter Values

The most recently assigned value of a parameter can be accessed like any other attrribute in Python, by using “dot notation” – that is, <Component>.<parameter>. For instance, the print statements in the print_after function of the example above use output.value and decision.value to access the value parameter of the output and decision Mechanisms, respectively (more specifically, they access the first element of the output Mechanism’s value, output.value[0], and the first and second elements of the decison Mechanism’s value). This returns their most recently assigned values. However, as an instance of the Parameters class, a parameter can be stateful, which means it can have more than one value associated with it. For example, PsyNeuLink has the capacity to execute the same Component in different contexts, either as part of different Compositions or, within the same Composition, as part of model-based simulations executed by the Composition’s controller. The value of a parameter in a particular context can be accessed by using the get method for the parameter and providing the context, for example:

>>> output.parameters.value.get('Stroop Model - Conflict Monitoring')[0]
[ 0.65  0.35]

Notice that, here, the name of the Composition in which the Mechanism was executed is used as the context; see Composition_Scope_of_Execution for additional information about how to specify contexts. If no context is specified, then the get method returns the most recently assigned value of the parameter, just like dot notation.

If a parameter is stateful, then its previous value can also be accessed, using the get_previous method; for example:

>>> output.parameters.value.get_previous('Stroop Model - Conflict Monitoring')[0]
[ 0.55  0.45]

Notice that the value returned is the one from Trial 2 in the example above, immediately prior to the last one run (Trial 3). By default, stateful parameters preserve only one previous value. However, a parameter can be specified to have a longer history, in which case get_previous can be used to access earlier values. For example, the following sets output Mechanism’s value parameter to store up to three previous values:

>>> output.parameters.value.history_max_length = 3

If included in the script above, then the following would return the output Mechanism’s value from two trials before the last one run:

>>> output.parameters.value.get_previous('Stroop Model - Conflict Monitoring', 2)[0]
[ 0.38 0.62]

Notice that this is the value from Trial 1 in the example above.

Setting Parameter Values

There are two different ways to set parameter values in PsyNeuLink, that correspond to the two ways of accessing their values discussed in the preceding section:

• “dot notation” – that is, <Component>.<parameter> = some_new_value

• the set method of the Parameter class; that is <Component>.parameters.<parameter>.set(<value>, <context>)).

In the case of non-stateful parameters, these two approaches behave equivalently, in which case it is easier and clearer to use dot notation.

Warning

In most cases, non-stateful parameters are intended to be configured automatically for a component upon instantiation by PsyNeuLink. Oftentimes, there are additional steps of validation and setup beyond simply assigning a value to some attribute of the component instance. Be cautious if you decide to manually set a non-stateful parameter.

In the case of stateful parameters (the most common type), assigning a value using dot notation and the set method can behave differently under some circumstances.

Dot notation is simpler, but assumes that the context for which the specified value should apply is the most recent context in which the Parameter’s owner Component has executed. If the value should apply to a different context, then the set method must be used, which allows explicit specification of the context. See below for examples of appropriate use cases for each, as well as explanations of contexts when executing Mechanisms and Compositions, respectively.

Warning

If a given component has not yet been executed, or has only been executed standalone without a user-provided context, then dot notation will set the Parameter’s value in the baseline context. Analogously, calling the set method without providing a context will also set the Parameter’s value in the baseline context. In either of these cases, any new context in which the Component executes after that will use the newly-provided value as the Parameter’s baseline.

Example use-cases for dot notation

• Run a Composition, then change the value of a component’s parameter, then run the Composition again with the new parameter value:

  >>> # instantiate the mechanism
  >>> m = ProcessingMechanism(name='m')
  >>> # create a Composition containing the Mechanism
  >>> comp1 = Composition(name='comp1', nodes=[m])
  >>> comp1.run(inputs={m:1})
  >>> # returns: [array([1.])]
  >>> # set slope of m1's function to 2 for the most recent context (which is now comp1)
  >>> m.function.slope.base = 2
  >>> comp1.run(inputs={m:1})
  >>> # returns: [array([2.])]
  >>> # note that changing the slope of m's function produced a different result
  >>> comp2 = Composition(name='comp2', nodes=[m])
  >>> comp2.run(inputs={m:1})
  >>> # returns: [array([1.])]
  >>> # because slope is a stateful parameter,
  >>> # executing the Mechanism in a different context is unaffected by the change
  

• Cautionary example: using dot notation before a component has been executed in a non-default context will change its value in the default context, which will in turn propagate to new contexts in which it is executed:

  >>> # instantiate the mechanism
  >>> m = ProcessingMechanism(name='m')
  >>> # create two Compositions, each containing m
  >>> comp1 = Composition(name='comp1', nodes=[m])
  >>> comp2 = Composition(name='comp2', nodes=[m])
  >>> m.execute([1])
  >>> # returns: [array([1.])]
  >>> # executing m outside of a Composition uses its default context
  >>> m.function.slope.base = 2
  >>> m.execute([1])
  >>> # returns: [array([2.])]
  >>> comp1.run(inputs={m:1})
  >>> # returns: [array([2.])]
  >>> comp2.run(inputs={m:1})
  >>> # returns: [array([2.])]
  >>> # the change of the slope of m's function propagated to the new Contexts in which it executes
  

Example use-cases for Parameter set method

• Change the value of a parameter for a context that was not the last context in which the parameter’s owner executed:

  >>> # instantiate the mechanism
  >>> m = ProcessingMechanism(name='m')
  >>> # create two Compositions, each containing m
  >>> comp1 = Composition(name='comp1', nodes=[m])
  >>> comp2 = Composition(name='comp2', nodes=[m])
  >>> comp1.run({m:[1]})
  >>> # returns: [array([1.])]
  >>> comp2.run({m:[1]})
  >>> # returns: [array([1.])]
  >>> # the last context in which m was executed was comp2,
  >>> # so using dot notation to change a parameter of m would apply only for the comp2 context;
  >>> # changing the parameter value for the comp1 context requires use of the set method
  >>> m.function_parameters.slope.set(2, comp1)
  >>> comp1.run({m:[1]})
  >>> # returns: [array([2.])]
  >>> comp2.run({m:[1]})
  >>> # returns: [array([1.])]
  

• Cautionary example: calling the set method of a parameter without a context specified changes its value in the default context which, in turn, will propagate to new contexts in which it is executed:

  >>> # instantiate the mechanism
  >>> m = ProcessingMechanism(name='m')
  >>> # create two Compositions, each containing m
  >>> comp1 = Composition(name='comp1', nodes=[m])
  >>> comp2 = Composition(name='comp2', nodes=[m])
  >>> comp1.run({m:[1]})
  >>> # returns: [array([1.])]
  >>> comp2.run({m:[1]})
  >>> # returns: [array([1.])]
  >>> # calling the set method without specifying a context will change the default value for new contexts
  >>> m.function_parameters.slope.set(2)
  >>> comp1.run({m: [1]})
  >>> # returns: [array([1.])]
  >>> # no change because the context had already been set up before the call to set
  >>> comp2.run({m:[1]})
  >>> # returns: [array([1.])]
  >>> # no change because the context had already been set up before the call to set
  >>> # set up a new context
  >>> comp3 = Composition(name='comp3', nodes=[m])
  >>> comp3.run({m: [1]})
  >>> # returns: [array([2.])]
  >>> # 2 is now the default value for the slope of m's function, so it now produces a different result
  

Function Parameters

The parameters attribute of a Component contains a list of all of its parameters. It is important here to recognize the difference between the parameters of a Component and those of its function. In the examples above, value is a parameter of the output and decision Mechanisms themselves. However, each of those Mechanisms also has a function; and, since those are PsyNeuLink Functions which are also Compoments, those too have parameters. For example, the output Mechanism was assigned the Logistic Function, which has a gain and a bias parameter (as well as others). The parameters of a Component’s function can also be accessed using dot notation, by referencing the function in the specification. For example, the current value of the gain parameter of the output's Logistic Function can be accessed in either of the following ways:

>>> output.function.gain.base
1.0
>>> output.function.parameters.gain.get()
1.0

Modulable Parameters

Some parameters of Components can be modulable, meaning they can be modified by another Component (specifically, a ModulatorySignal belonging to a ModulatoryMechanism). If the parameter of a Mechanism or a Projection is modulable, it may be assigned a ParameterPort – this is a Component that belongs to the Mechanism or Projection and can receive a Projection from a ModulatorySignal, allowing another component to modulate the value of the parameter. ParameterPorts are created for every modulable parameter of a Mechanism, its function, any of its secondary functions, and similarly for Projections. These determine the value of the parameter that is actually used when the Component is executed, which may be different than the base value returned by accessing the parameter directly (as in the examples above); see Modulation for a more complete description of modulation. The current modulated value of a parameter can be accessed from the value of the corresponding ParameterPort. For instance, the print statement in the example above used task.parameter_ports[GAIN].value to report the modulated value of the gain parameter of the task Mechanism’s Logistic function when the simulation was run. For convenience, it is also possible to access the value of a modulable parameter via dot notation. Dot notation for modulable parameters is slightly different than for non-modulable parameters to provide easy access to both base and modulated values:

>>> task.function.gain
(Logistic Logistic Function-5):
    gain.base: 1.0
    gain.modulated: [0.55]

Instead of just returning a value, the dot notation returns an object with base and modulated attributes. modulated refers to the value of the ParameterPort for the parameter:

>>> task.parameter_ports[GAIN].value
[0.62]
>>> task.gain.modulated
[0.62]

This works for any modulable parameters of the Mechanism, its function, or secondary functions. Note that, here, neither the parameters nor the function attributes of the Mechanism need to be included in the reference. Note also that, as explained above, the value returned is different from the base value of the function’s gain parameter:

>>> task.function.gain.base
1.0

This is because when the Compoistion was run, the control Mechanism modulated the value of the gain parameter.

Some Parameters may be modulable, but not modulated by a ParameterPort, because ParameterPorts are only created for Parameters whose values are numeric at the time of Component construction. For example, TransferMechanism.termination_threshold has a default value of None and will not have a ParameterPort by default. Similarly, when noise is set to a function or value containing a function, it will not have an associated ParameterPort.

In this case, dot notation for these modulable Parameters will behave the same as for non-modulable Parameters.

Displaying and Logging Values

Displaying values The console output in the example above was generated using the call_after_trial argument in the Composition’s run method, that calls the print_after function defined in Python. There are other similar “hooks” in the run method that can be used not only to monitor values, but also to carry out custom operations at various points during execution (before and/or after each run, run or execution of the Components in a trial).

Logging values. PsyNeuLink also has powerful logging capabilities that can be used to track and report any parameter of a model. For example, including the following lines in the script for Stroop_model, after the task and control Mechanisms are constructed:

task.log.set_log_conditions(VALUE)
control.log.set_log_conditions(VARIABLE)
control.log.set_log_conditions(VALUE)

logs the value of the control and task Mechanisms each time they are executed. Information in the log can be printed to the console using its print_entries method, and specifying the desired information in its display argument. For example, calling the following after Stroop_model.run has been called:

Stroop_model.log.print_entries(display=[TIME, VALUE])

generates the following report of the time at which the control and task Mechanisms were executed and their value for each execution (only the first two trials worth of the output are reproduced here):

Log for Stroop Model:

Logged Item:   Time          Value

'CONTROL'      0:0:10:0     [[0.51]]
'CONTROL'      0:1:10:0     [[0.59]]
...

'TASK'         0:0:0:1      [[0.57 0.56]]
'TASK'         0:0:1:1      [[0.58 0.55]]
'TASK'         0:0:2:1      [[0.59 0.55]]
'TASK'         0:0:3:1      [[0.6  0.54]]
'TASK'         0:0:4:1      [[0.61 0.54]]
'TASK'         0:0:5:1      [[0.62 0.53]]
'TASK'         0:0:6:1      [[0.63 0.53]]
'TASK'         0:0:7:1      [[0.64 0.52]]
'TASK'         0:0:8:1      [[0.65 0.51]]
'TASK'         0:0:9:1      [[0.67 0.51]]
'TASK'         0:1:0:1      [[0.68 0.5 ]]
'TASK'         0:1:1:1      [[0.69 0.49]]
'TASK'         0:1:2:1      [[0.71 0.48]]
'TASK'         0:1:3:1      [[0.72 0.47]]
'TASK'         0:1:4:1      [[0.74 0.46]]
'TASK'         0:1:5:1      [[0.75 0.45]]
'TASK'         0:1:6:1      [[0.77 0.44]]
'TASK'         0:1:7:1      [[0.78 0.42]]
'TASK'         0:1:8:1      [[0.8  0.41]]
'TASK'         0:1:9:1      [[0.81 0.4 ]]
...

The time is reported as run:trial:pass:time_step. Note that there is only one entry for the control Mechanism per trial, since it is executed only once per trial; but there are ten entries for the task Mechanism for each trial since it executed ten times, as specified in the Conditions described above.

The output of a Log can also be reported in various other formats, including as a numpy array (using its nparray method, as a dictionary of values for each entry (using its nparray_dictionary method), and in CSV format (using its csv method.

Learning

Needless to say, no framework for modeling brain and/or cognitive function is complete without implementing learning mechanisms. PsyNeuLink does so in two ways: in a native form, and by integrating tools available from other Python-based environments. Currently, PsyNeuLink has builtin intregration with PyTorch, however other envirnoments can be accessed using UserDefinedFunctions. Since such environments are becoming increasingly accessible and powerful, the native implementation of learning in PsyNeuLink is designed with a complementary set of goals: modularity and exposition, rather than efficiency of computation. That is, it is better suited for “story-boarding” a model that includes learning components, and for illustrating process flow during learning, than it is for large scale simulations involving learning. However, the specification of the learning components of a model in PsyNeuLink can easily be translated into a Pytorch description, which can then be integrated into the PsyNeuLink model with all the benefits of Pytorch execution. Each of the two ways of specifying learning components is described below.

LearningMechanisms

PsyNeuLink has a native class – LearningMechanism – that can be used to implement various forms of learning, including unsupervised forms (such as Hebbian) and supervised forms (such as reinforcement learning and backpropagation). LearningMechanisms take as their input a target and/or an error signal, provided by a MappingProjection from the source of the error signal (either a ComparatorMechanism or another LearningMechanism). LearningMechanisms use LearningSignals (a type of OutputPort) to send a LearningProjection to the MappingProjection that is being learned. The type of learning implemented by a LearningMechanism is determined by the class of LearningFunction assigned as its function. In some cases (such as multilayered backpropagation networks), configuration of the LearningMechanisms and corresponding Projections can become complex; PsyNeuLink provides methods for implementing these automatically, which also serves to illustrate the flow of signals and errors implemented by the algorithm. The example below implements learning in a simple three-layered neural network that learns to compute the X-OR operation:

# Construct Processing Mechanisms and Projections:
input = ProcessingMechanism(name='Input', default_variable=np.zeros(2))
hidden = ProcessingMechanism(name='Hidden', default_variable=np.zeros(10), function=Logistic())
output = ProcessingMechanism(name='Output', default_variable=np.zeros(1), function=Logistic())
input_weights = MappingProjection(name='Input Weights', matrix=np.random.rand(2,10))
output_weights = MappingProjection(name='Output Weights', matrix=np.random.rand(10,1))
xor_comp = Composition('XOR Composition')
learning_components = xor_comp.add_backpropagation_learning_pathway(
                                                pathway=[input, input_weights, hidden, output_weights, output])
target = learning_components[TARGET_MECHANISM]

# Create inputs:            Trial 1  Trial 2  Trial 3  Trial 4
xor_inputs = {'stimuli':[[0, 0],  [0, 1],  [1, 0],  [1, 1]],
              'targets':[  [0],     [1],     [1],     [0] ]}
xor_comp.learn(inputs={input:xor_inputs['stimuli'],
                     target:xor_inputs['targets']})

Calling the Composition’s show_graph with show_learning=True shows the network along with all of the learning components created by the call to add_backpropagation_pathway:

XOR Model. Items in orange are learning components implemented by the call to add_backpropagation_pathway; diamonds represent MappingProjections, shown as nodes so that the Learning Projections to them can be shown.

Training the model requires specifying a set of inputs and targets to use as training stimuli, and identifying the target Mechanism (that receives the input specifying the target responses):

# Construct 4 trials worth of stimuli and responses (for the four conditions of the XOR operation):
xor_inputs = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
xor_targets = np.array([ [0],   [1],     [1],    [0]])

# Identify target Mechanism returned by add_backpropation_pathway called above
target_mech = learning_components[TARGET_MECHANISM]

# Run the model:
result = xor_model.learn(inputs={input_mech:xor_inputs,
                               target_mech:xor_targets},
                       num_trials=2)

It can also be run without learning by calling the run method with enable_learning=False.

The model shown above implements learning for a simple linear path. However, virtually any model can be created using calls to a Composition’s learning methods to build up more complex pathways. For example, the following implements a network for learning semantic representations described in Rumelhart & Todd, 1993 (pdf):

#  Represention  Property  Quality  Action
#           \________\_______/_______/
#                        |
#                 Relations_Hidden
#                   _____|_____
#                  /           \
#   Representation_Hidden  Relations_Input
#               /
#   Representation_Input

# Construct Mechanisms
rep_in = pnl.ProcessingMechanism(input_shapes=10, name='REP_IN')
rel_in = pnl.ProcessingMechanism(input_shapes=11, name='REL_IN')
rep_hidden = pnl.ProcessingMechanism(input_shapes=4, function=Logistic, name='REP_HIDDEN')
rel_hidden = pnl.ProcessingMechanism(input_shapes=5, function=Logistic, name='REL_HIDDEN')
rep_out = pnl.ProcessingMechanism(input_shapes=10, function=Logistic, name='REP_OUT')
prop_out = pnl.ProcessingMechanism(input_shapes=12, function=Logistic, name='PROP_OUT')
qual_out = pnl.ProcessingMechanism(input_shapes=13, function=Logistic, name='QUAL_OUT')
act_out = pnl.ProcessingMechanism(input_shapes=14, function=Logistic, name='ACT_OUT')

# Construct Composition
comp = Composition(name='Rumelhart Semantic Network')
comp.add_backpropagation_learning_pathway(pathway=[rel_in, rel_hidden])
comp.add_backpropagation_learning_pathway(pathway=[rel_hidden, rep_out])
comp.add_backpropagation_learning_pathway(pathway=[rel_hidden, prop_out])
comp.add_backpropagation_learning_pathway(pathway=[rel_hidden, qual_out])
comp.add_backpropagation_learning_pathway(pathway=[rel_hidden, act_out])
comp.add_backpropagation_learning_pathway(pathway=[rep_in, rep_hidden, rel_hidden])
comp.show_graph(show_learning=True)

The figure below shows this network with all of its learning components:

Rumelhart Semantic Network. Items in orange are learning components implemented by the calls to add_backpropagation_pathway; diamonds represent MappingProjections, shown as nodes so that the Learning Projections to them can be shown.

Given the number of learning components, training the model above using standard PsyNeuLink components can take a considerable amount of time. However, the same Composition can be implemented using the AutodiffComposition, by replacing the relevant line in the example above with comp = AutoComposition(name='Rumelhart Semantic Network')). The AutodiffComposition uses PyTorch to execute learning, which runs considerably (as much as three orders of magnitude) faster (see Learning in a Composition, as well as Learning Using AutodiffCompositon for comparisons of the advantages and disadvantages of using a standard Composition vs. AutodiffComposition for learning).

Customization

The Mechanisms in the examples above all use PsyNeuLink Functions. However, as noted earlier, a Mechanism can be assigned any Python function, so long as it is compatible with the Mechanism’s type. More specifically, its first argument must accept a variable that has the same shape as the Mechanism’s variable. For most Mechanism types this can be specified in the default_variable argument of their constructors, so in practice this places little constraint on the type of functions that can be assigned. For example, the script below defines a function that returns the amplitude of a sinusoid with a specified frequency at a specified time, and then assigns this to a ProcessingMechanism:

>>> def my_sinusoidal_fct(input=[[0],[0]],
...                       phase=0,
...                       amplitude=1):
...    frequency = input[0]
...    time = input[1]
...    return amplitude * np.sin(2 * np.pi * frequency * time + phase)
>>> my_wave_mech = pnl.ProcessingMechanism(default_variable=[[0],[0]],
...                                        function=my_sinusoidal_fct)

Note that the first argument is specified as a 2d variable that contains the frequency and time values as its elements – this matches the definition of the ProcessingMechanism’s default_variable, which the Mechanism will expect to receive as input from any other Mechanisms that project to it. When a Python function is specified as the function of Mechanism (or any other Component in PsyNeuLink), it is automatically “wrapped” as a UserDefinedFunction, a special class of PsyNeuLink Function that integrates it with PsyNeuLink: in addition to making its first argument available as the input to the Component to which it is assigned, it also makes its parameters available for modulation by ControlMechanisms. For example, notice that my_sinusoidal_fct has two other arguments, in addition to its input: phase and amplitude. As a result, the phase and amplitude of my_wave_mech can be modulated in by referencing them in the constructor of a ControlMechanism:

>>> control = ControlMechanism(control_signals=[('phase', my_wave_mech),
                                                 'amplitude', my_wave_mech])

This facility not only makes PsyNeuLink flexible, but can be used to extend it in powerful ways. For example, as mentioned under Learning, functions from other environments that implement complex learning models can be assigned as the function of a Mechanism, and in that way integrated into a PsyNeuLink model.

Conclusion

The examples above are intended to provide a sample of PsyNeuLink’s capabilities, and how they can be used. The Tutorial provides a more thorough, interactive introduction to its use, and the User's Guide provides a more detailed description of PsyNeuLink’s organization and capabilities.