Dopamine and Temporal Differences Learning (Montague, Dayan & Sejnowski, 1996)¶
“A framework for mesencephalic dopamine systems based on predictive Hebbian learning.”
Overview¶
This model implements the comparison of a theory of mesencephalic dopamine system function based on predictive Hebbian learning to physiological monkey data as found in Montague, Dayan, and Sejnowski, 1996.
In this paper, Montague, Dayan, and Sejnowski proposed that one way in which animals learn is through making predictions and then adapting behavior based on the errors in the prediction. This model is derived from ideas previously presented by Sutton et. al. and Rescorla & Wagner.
The figures below are PsyNeuLink recreations of figures 5A-C in the original paper, which show a “model for mesolimbic dopamine cell activity during monkey conditioning. The first plot shows ∂(t) over time for three trials during training. The second plot shows ∂(t) over all 100 trials of the model responses, with training beginning at trial 10. In these plots, the reward was withheld every 15 trials to simulate mistakes. The third plot demonstrates extinction of response to the stimulus due to non-delivery of the reward after trial 70.
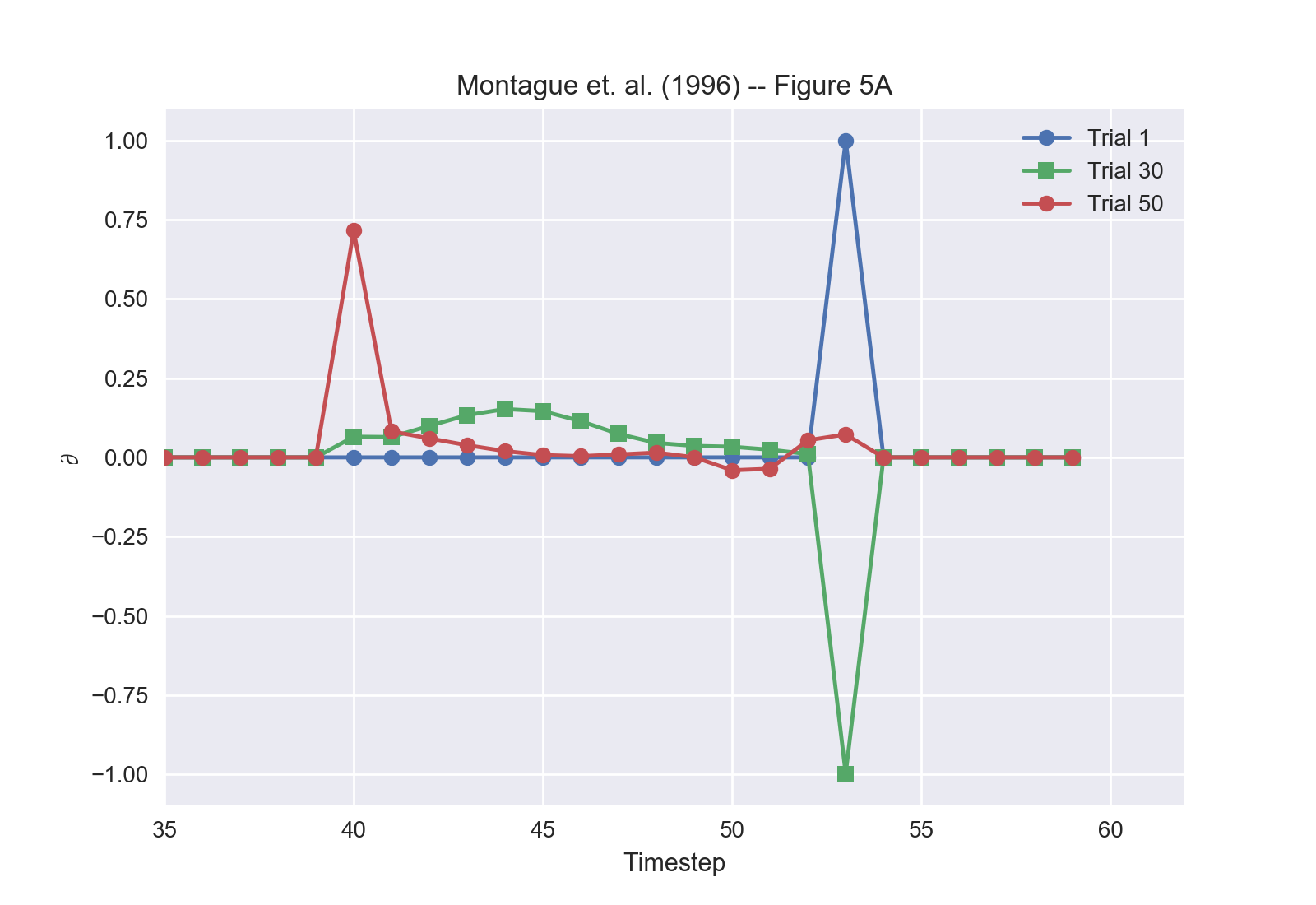
Figure 5A¶
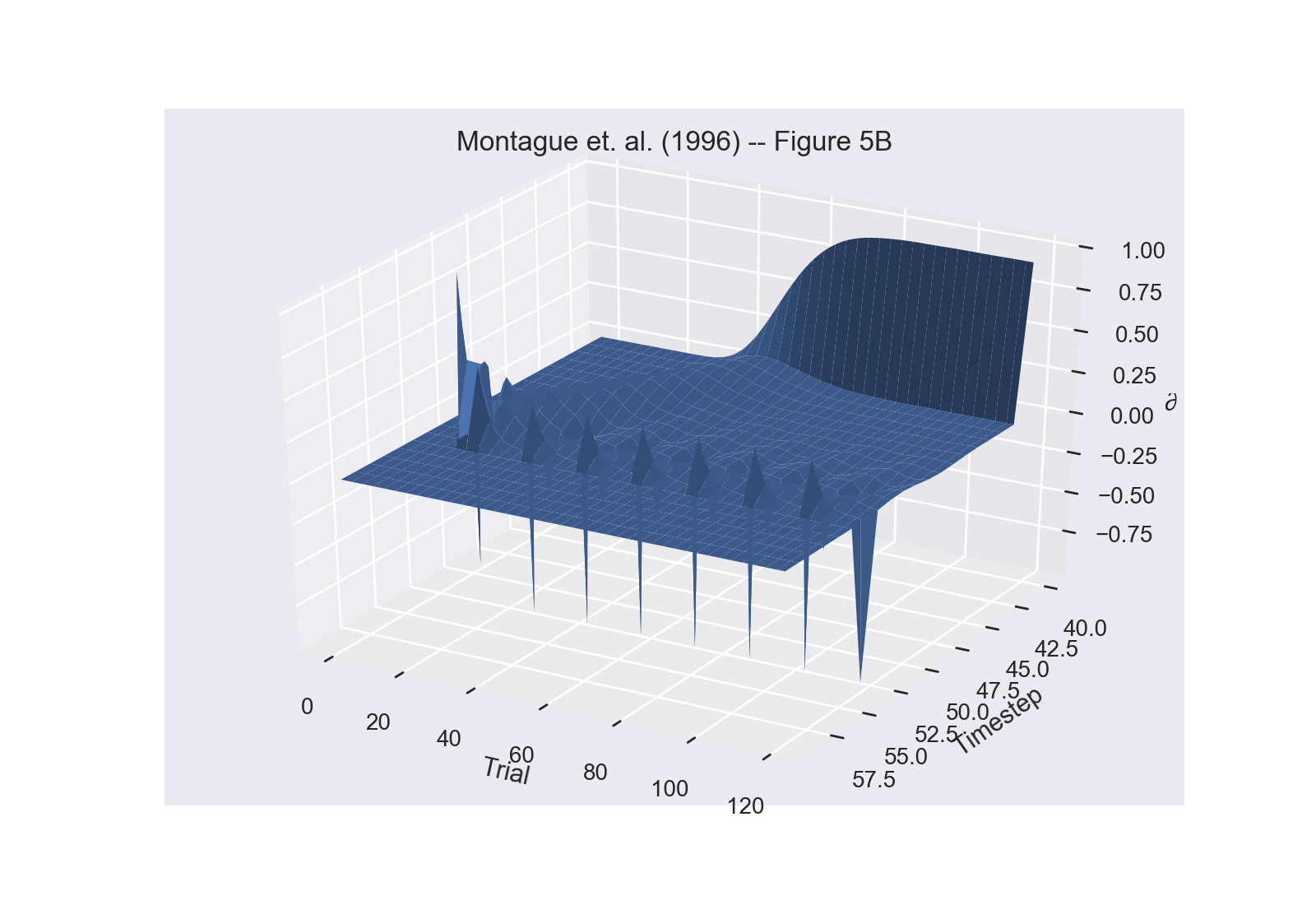
Figure 5B¶
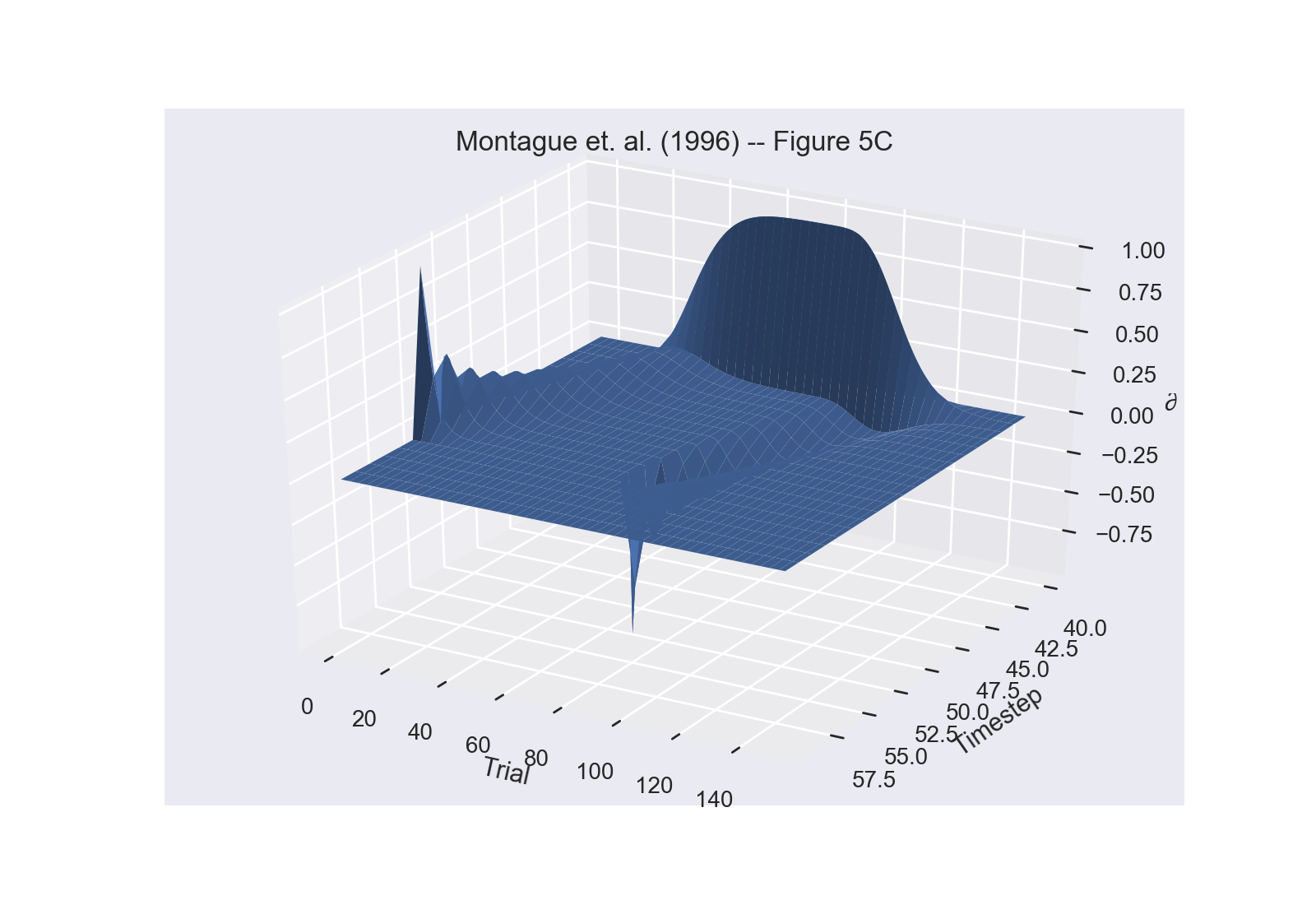
Figure 5C¶
The Model¶
The basic setup for the model requires a Transfer Mechanism for sample delivery, a TransferMechanism for action selection, a MappingProjection to connect the two TransferMechanisms, and a LearningProjection to execute the learning aspect of the model.
The MappingProjection represents the weights; thus, the
projection’s matrix is initialized to all zeros. The
LearningProjection is initialized with
TDLearning as its learning_function; this directs the process
containing this LearningProjection to initialize a
PredictionErrorMechanism instead of a regular
ComparatorMechanism. All of the functions in the script
use the same basic setup with adaptations made to the samples and targets
provided to correspond to the aspect of the experiment that they are modeling.
The model can be visualized as shown below.
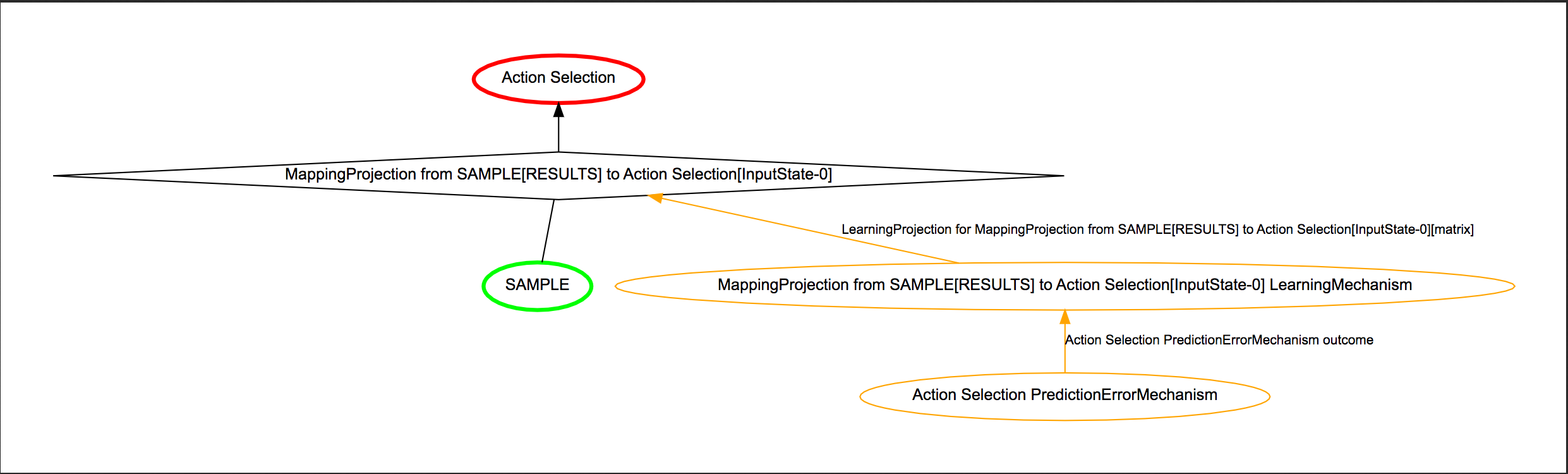
System graph¶
Script: Download MontagueModel.py