FIELDLINES

Table of Contents

Theory
Compilation
Input Data Format
Execution
Output Data Format
Visualization
Tutorials

The FIELDLINES code follows field lines in a toroidal domain given a vacuum, VMEC, PIES, or SPEC equilibria, and is parallelized over the field line trajectories.

Theory

The FIELDLINES code follows fieldlines in a toroidal domain. This is achieved by placing the magnetic field on an R-phi-Z mesh and constructing splines over that mesh. An ODE for following field lines as a function of the toroidal angle can be constructed by relating the motions in R and Z as a function of phi through

\(\frac{\partial R}{\partial \phi} = R\frac{B_R}{B_\phi}\) and \(\frac{\partial Z}{\partial \phi} = R\frac{B_Z}{B_\phi}\)

In this representation the trajectory of the fieldline can be parameterized by toroidal angle. The resulting ODE is solved with a user determined step-size and accuracy. The available ODE packages are: LSODE, NAG D02CJF(requires license), and a Runge-Kutta-Hutta 6-th order 8 step method (D. Sarafyan, J. Math. Anal. Appl. 40, 436-455 (1972)) . The calculation of field line trajectories is parallelized over each field line. Thus each processor can follow each field line independently to speed computation. It should be noted that PHI_END and PHI_START define the direction of integration. The -reverse flag is present to aide in switching the sign of PHI_END automatically.

The code assembles fields from various sources. The vacuum component of the field can be calculated directly from a coils file or an mgrid file. In the later case the FIELDLINES grid must match the mgrid file. The plasma field inside the equilibria domain is placed directly on the background grid. The plasma response external to the equilibria is calculated using a virtual casing principle. In order to maintain accuracy near the surface of the plasma, the virtual casing principle employs an adaptive integration scheme over the surface current. This scheme is either handled by NAG D01EAF (if available), or the DCUHRE algorithm (J. Berntsen, T. O. Espelid and A. Genz, Trans. Math. Softw. 17 (1991), pp. 437-451., J. Berntsen, T. O. Espelid and A. Genz, Trans. Math. Softw. 17 (1991), pp. 452-456.) . This part of the code is parallelized over the vertical dimension (Z). Thus the z-axis is domain decomposed.

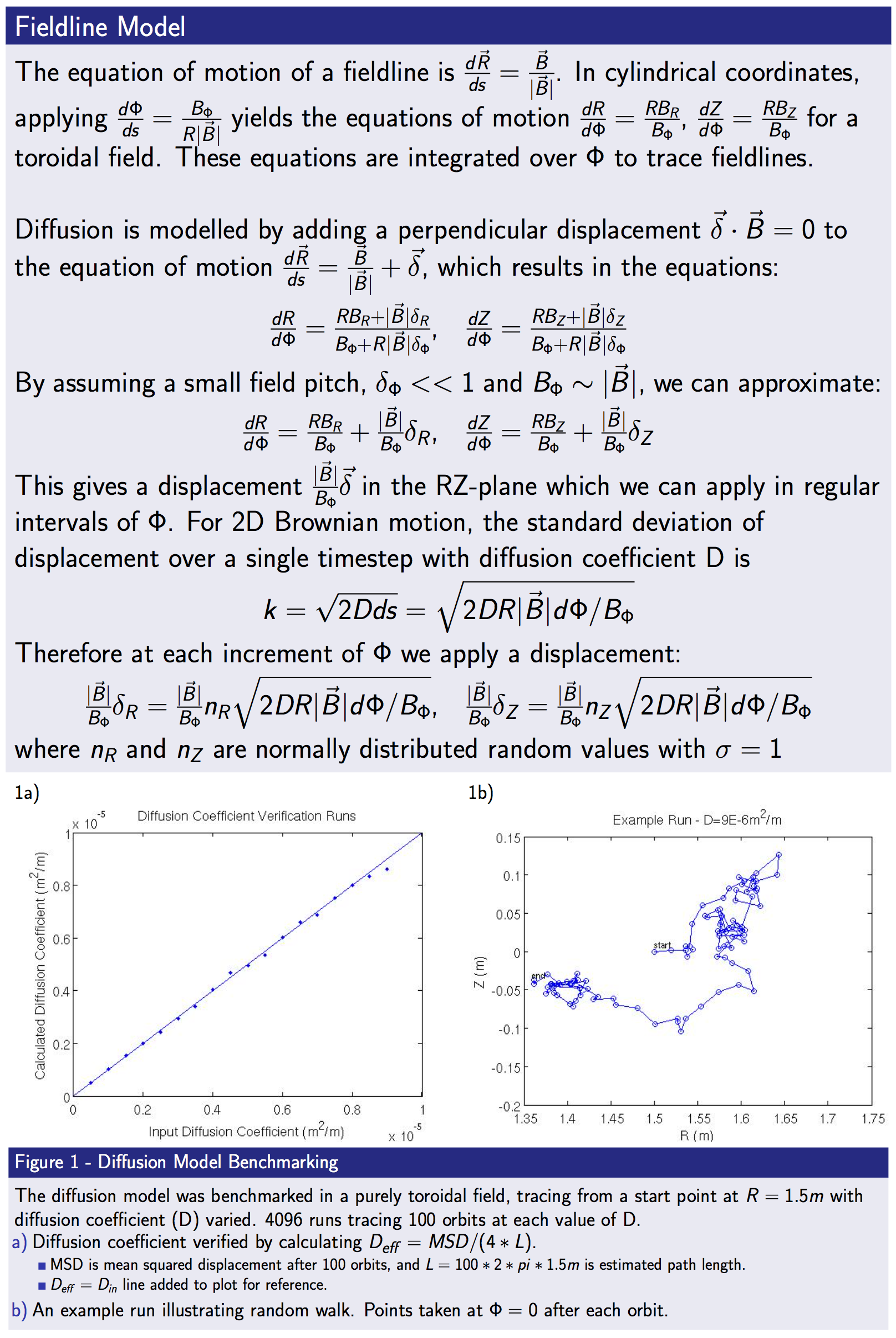
The code can also be given a limiting surface (vessel, first wall, divertor). Field lines which pass through this surface are not followed beyond that point. An artificial diffusion can also be applied to aid in modeling divertor strike points.

If the user wishes, the code can automatically locate the magnetic axis, find the 'edge' of the flux surfaces, and output the periodic orbit of the edge with the -full option. Here the code begins by first following fieldlines from the minimum and maximum values in R_START and Z_START. A magnetic axis is identified using a periodic orbit search. The edge is then refined once so any edge stochastic region may be resolved. The code then follows fieldlines in this domain from the axis to the 'edge.' If the user supplies an R,PHI,Z guess for the edge periodic orbit the code will find it and the associated separatrix.

Compilation

FIELDLINES is a component of the STELLOPT suite of codes. It is contained within the 'stellopt.zip' file. Compilation of the STELLOPT suite is discussed on the STELLOPT Compilation Page. To obtain the code please contact the author Samuel A. Lazerson (lazerson@pppl.gov).

Input Data Format

The FIELDLINES code is controled through command line inputs and an input namelist which should be placed in the input.ext file. While the entire VMEC input name is not required the EXTCUR array is required. The name lists should look like:

#!fortran
&INDATA
 ! VMEC input namelist (only need coil currents for usual runs)
 EXTCUR(1) = 10000.00
 EXTCUR(2) = 10000.00
 EXTCUR(3) = 12000.00
 EXTCUR(4) = 12000.00
 EXTCUR(5) = 6000.00
 ! VMEC Axis info (for putting a current on axis -axis option)
 !     This information is utilized if you want to place the net toroidal current
 !     on a magnetic axis.  Useful for doing vacuum tokamak equilibria
 CURTOR = 5000.0
 NFP = 5
 NTOR = 6
 RAXIS = 3.6  0.1 0.001
 ZAXIS = 0.0  0.1 0.001
/
&FIELDLINES_INPUT
 NR = 251                          ! Number of radial gridpoints
 NPHI = 36                         ! Number of toroidal gridpoints
 NZ = 301                          ! Number of vertical gridpoints
 RMIN = 2.5                        ! Minimum extent of radial grid
 RMAX = 5.0                        ! Maximum extent of radial grid
 ZMIN = -1.5                       ! Minimum extent of vertical grid
 ZMAX = 1.5                        ! Maximum extent of vertical grid
 PHIMIN = 0.0                      ! Minimum extent of toroidal grid, overridden by mgrid or coils file
 PHIMAX = 0.628                    ! Maximum extent of toroidal grid, overridden by mgrid or coils file
 MU = 0.0                          ! Fieldline diffusion (mu=D/v) [m^2/m]
 R_START =  3.6  3.7  3.8          ! Radial starting locations of fieldlines
 Z_START =  0.0  0.0  0.0          ! Vertical starting locations of fieldlines
 PHI_START =  0.0  0.0  0.0        ! Toroidal starting locations of fieldlines (radians)
 PHI_END =  629.0  629.0  629.0    ! Maximum distance in toroidal direction to follow fieldlines
 NPOINC = 72                       ! Number of toroidal points per-period to output the field line trajectory
 INT_TYPE = 'NAG'                  ! Fieldline integration method (NAG, RKH68, LSODE)
 FOLLOW_TOL = 1.0E-12              ! Fieldline following tollerance
 VC_ADAPT_TOL = 1.0E-7             ! Virtual casing tolerance (if using plasma field from equilibria)
 R_HC = 3.5                        ! R Location of periodic orbit (-full)
 Z_HC = 0.5                        ! Z Location guess for periodic orbit (-full)
 PHI_HC = 0.0                      ! PHI Location for periodic orbit(-full)
 NUM_HCP = 512                     ! Number of points for separatrix plot (-full)
 DELTA_HC = 1.0E-4                ! Initial length of separatrix line (-full)
/
&END

If you wish to model an NFP=1 system please comment out the PHIMAX line (this sets PHIMAX to 2*pi to machine precision). If you system has an underlying field symmetry (such as a stellarator) please make sure the choice of NPHI is consistent. For example a 5 field period machine which was modeled with NFP=5 and NPHI=36, would require NPHI=176 and NFP=1 for consistency. This places a spline knot at every point in the original 5 field period model. In general the formula is NPHI1=(NPHI-1)*NFP+1, where NPHI1 is the full device model (nphi) and NPHI is the field period model (nphi).

The MU diffusion coefficient has units of [m^2/m]. To convert the traditional diffusion coefficient D [m^2/s] to MU you simply divide D by the typical velocity (usually the sound speed) of your particle.

Execution

The FIELDLINES code is controlled through a combination of command-line inputs and an input namelist. The input namelist must be in the equilibrium input file. That file must also contain the VMEC INDATA namelist (although only the EXTCUR array will be used). The FIELDLINES code is run from the command line taking an equilibrium input file as a necessary argument. This input file must have the INDATA (for EXTCUR) and FIELDLINES_IN namelists in it.

XFIELDLINES -vmec <VMEC FILE> -pies <PIES_FILE> -spec <SPEC FILE> -coil <COIL FILE> -mgrid <MGRID FILE> -vessel <VESSEL FILE> -vac -full -noverb -help

Argument	Default	Description
-vmec	NONE	VMEC input extension
-pies	NONE	PIES input extension
-spec	NONE	SPEC input extension
-coil	NONE	Coils File
-mgrid	NONE	Makegrid style vacuum grid file
-vessel	NONE	First wall file
-screen	NONE	Poincaré Screen file
-vac	NONE	Only compute the vacuum field
-hitonly	NONE	Only save strikepoint locations (used in conjunction with -vessel)
-full	NONE	Auto calculate axis and edge maximum resolution
-reverse	NONE	Follow particles in oposite direction.
-edge	NONE	Place all starting points at VMEC boundary.
-field	NONE	Outputs the B-Field on the cylindrical grid only.
-raw	NONE	Treats EXTCUR array as raw values (EXTCUR is a scale factor applied to what's in the coils file).
-auto	NONE	Starting points set equal to radial grid and run from the min to max values of R_START and Z_START
-field_start	NONE	Extension and fieldline number to use for initializing run.
-noverb	NONE	Suppresses screen output
-help	NONE	Print help message

In it's simplest invokation the code requires a VMEC input file and some source of vacuum field. Please note that FIELDLINES takes advantage of shared memory MPI so the user must request full nodes

>mpirun -N 6 ~/bin_847/xfieldlines -vmec ncsx_c09r00_free -mgrid mgrid_c09r00.nc -vac
FIELDLINES Version 0.50
----- Input Parameters -----
   FILE: input.ncsx_c09r00_free
   R   = [ 0.43600, 2.43600];  NR:    201
   PHI = [ 0.00000, 2.09440];  NPHI:   36
   Z   = [-1.00000, 1.00000];  NR:    201
   # of Fieldlines:   40
   VACUUM FIELDS ONLY!
----- MGRID Information -----
   FILE:mgrid_c09r00.nc
   R   = [ 0.43600, 2.43600];  NR   =  201
   PHI = [ 0.00000, 2.09440];  NPHI =   37
   Z   = [-1.00000, 1.00000];  NZ   =  201
----- FOLLOWING FIELD LINES -----
      Method: NAG
       Lines:   40
         Tol: 0.1000E-08  Type: M
   Delta-phi: 0.1745E-01
       Lines:  359989
----- WRITING DATA TO FILE -----
   FILE: fieldlines_ncsx_c09r00_free.h5
----- FIELDLINES DONE -----

Output Data Format

The FIELDLINES code outputs data in the HDF5 data format. The trajectory of each field line and relevant quantities for each run are stored in a fieldline_ext.h5 file. A MATLAB routine for reading the HDF5 file is available (MATLAB File Exchange: read_fieldlines.m). A sample of the HDF5 data structure looks like:

HDF5 "fieldlines_ncsx_c09r00_free.h5" {
GROUP "/" {
   DATASET "B_R" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 201, 36, 201 ) / ( 201, 36, 201 ) }
   }
   DATASET "B_Z" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 201, 36, 201 ) / ( 201, 36, 201 ) }
   }
   DATASET "PHI_lines" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 359990, 40 ) / ( 359990, 40 ) }
   }
   DATASET "R_lines" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 359990, 40 ) / ( 359990, 40 ) }
   }
   DATASET "Z_lines" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 359990, 40 ) / ( 359990, 40 ) }
   }
   DATASET "lcoil" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "lmgrid" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "lmu" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "lpies" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "lspec" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "lvac" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "lvessel" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "lvmec" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "nlines" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "nphi" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "npoinc" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "nr" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "nsteps" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "nz" {
      DATATYPE  H5T_STD_I32LE
      DATASPACE  SIMPLE { ( 1 ) / ( 1 ) }
   }
   DATASET "phiaxis" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 36 ) / ( 36 ) }
   }
   DATASET "raxis" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 201 ) / ( 201 ) }
   }
   DATASET "zaxis" {
      DATATYPE  H5T_IEEE_F64LE
      DATASPACE  SIMPLE { ( 201 ) / ( 201 ) }
   }
}
}

Visualization

Various visualization packages exist which can read the HDF5 file. Each field line is defined as a set of points in R phi and Z.

Tutorials

FIELDLINES Vacuum NCSX Tutorial

FIELDLINES NCSX Tutorial